Vì `SCD` cân tại `S=>SI \bot CD`
Trong `(SCD)` có: `SI \bot CD`
`=>d(S,CD)=SI=[a\sqrt{3}]/2`
Vì `SCD` cân tại `S=>SI \bot CD`
Trong `(SCD)` có: `SI \bot CD`
`=>d(S,CD)=SI=[a\sqrt{3}]/2`

Hãy giúp mình giải bài này với lời giải chi tiết và trình bày rõ ràng, mình cảm ơn ạ
Cho tứ diện đều ABCD cạnh a, có tâm của đáy là O. Tính khoảng cách:
a) Từ O đến (ACD)
b) Từ M đến (ABD) với M là trung điểm CD
c) Từ AB đến CD
Cho hình chóp S.ABCD có tam giác SAB đều và nằm trong mặt phẳng vuông góc với (ABCD) , tứ giác ABCD là hình vuông cạnh a . Gọi H là trung điểm của AB . Tính khoảng cách từ điểm H đến mặt phẳng (SCD).
Cho hình chóp S.ABCD có tam giác SAB đều và nằm trong mặt phẳng vuông góc với (ABCD) , tứ giác ABCD là hình vuông cạnh a . Gọi H là trung điểm của AB . Tính khoảng cách từ điểm H đến mặt phẳng (SCD).
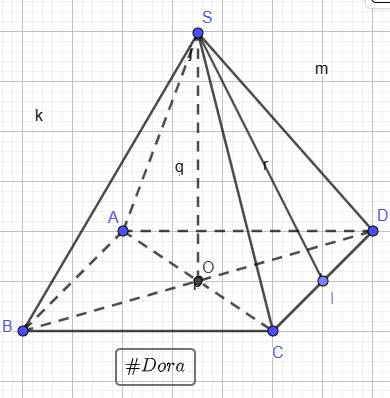
cho hình chóp tứ giác đều S.ABCD có ABCD là hình vuông tâm O. SB tạo với đáy một góc \(30^o\) . Tính khoảng cách từ O đến mp(SAD)
Bài 1: Cho hình chóp đều S.ABCD có AB=\(a\); SA=\(a\sqrt{2}\). P là trung điểm CD. Tính khoảng cách từ P đến mặt phẳng (SAB)
Bài 2: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A. AB= \(a\sqrt{2}\) ; I là trung điểm BC. Hình chiếu vuông góc H của S lên mặt phẳng (ABC) thỏa mãn\(\overrightarrow{IA}=-2\overrightarrow{IH}\) . Góc giữa SC và (ABC) = 60°. K là trung điểm AB. Tính khoảng cách từ K đến (SAH)
Cho hình chóp tam giác đều SABC có cạnh đáy bằng 2a và chiều cao bằng a√3. Gọi P là trung điểm của SA. Khoảng cách từ điểm P đến mặt phẳng (SBC) bằng Mọi người giúp mk với ạ. Mk cảm ơn
Cho hình chóp S.ABCD đáy là hình chữ nhật AB=a AD=2a, SA=a và vuông góc với đáy. Gọi M và I lần lượt trung điểm của SC và CD. Tính khoảng cách từ A đến (SBM)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tâm giác SAB đều và nằm trong mặt phẳng đáy. Tính khoảng cách từ điểm S đến mặt phẳng (ABC)