b: \(AC^2-HC^2=AH^2\)
\(AB^2-BH^2=AH^2\)
Do đó: \(AC^2-HC^2=AB^2-HB^2\)
hay \(AC^2+HB^2=AB^2+HC^2\)
b, Ta có \(AC^2-HC^2=AH^2;AB^2-HB^2=AH^2\left(pytago\right)\)
Do đó \(AC^2-CH^2=AB^2-HB^2\)
\(\Rightarrow AC^2+HB^2=AB^2+HC^2\)
b: \(AC^2-HC^2=AH^2\)
\(AB^2-BH^2=AH^2\)
Do đó: \(AC^2-HC^2=AB^2-HB^2\)
hay \(AC^2+HB^2=AB^2+HC^2\)
b, Ta có \(AC^2-HC^2=AH^2;AB^2-HB^2=AH^2\left(pytago\right)\)
Do đó \(AC^2-CH^2=AB^2-HB^2\)
\(\Rightarrow AC^2+HB^2=AB^2+HC^2\)
Các bạn giúp mình câu cuối với ạ
Giải giúp vs hứa cho 5*ạ: cho tam giác ABC vuông A đường cao AH.kẻ HE.vuôngAB,HD vuông AC. a) AB=6,Ac=8.tính bc.hc.bh.ah b) EA.AB=AD.AC=BH.HC c) AE.EB+AD.DC=AH² d) BE = BC.sin³C làm câu d thôi ạ
GIÚP EM CÂU C VỚI Ạ,EM CẦN GẤPP
Cho tam giác ABD, AB=6cm, AD=8cm, BD=10cm. Đường cao AH
a) Chứng minh tam giác ABD vuông. Tính MA, MB
b) Qua B kẻ Bx song song AD, Bx cắt AM tại C. Chứng minh AM.AC=BM.BD
c) CE cắt BD tại I, CE vuông góc AD. Chứng minh BM2=MI.MD
B= \(\dfrac{2\sqrt{3+\sqrt{5}-\sqrt{13}+\sqrt{48}}}{\sqrt{6}-\sqrt{2}}\)
GIÚP MÌNH VỚI Ạ
Giải giúp vs hứa cho 5*ạ: cho tam giác ABC vuông A đường cao AH.kẻ HE.vuôngAB,HD vuông AC. a) AB=6,Ac=8.tính bc.hc.bh.ah b) EA.AB=AD.AC=BH.HC c) AE.EB+AD.DC=AH² d) BE = BC.sin³C làm câu D thôi
Giúp với ạ
giảng hộ em câu 5 với ạ

giúp em với ạ
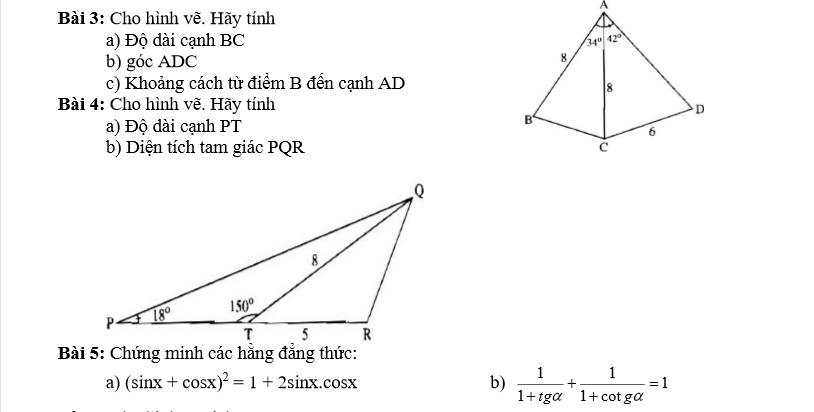
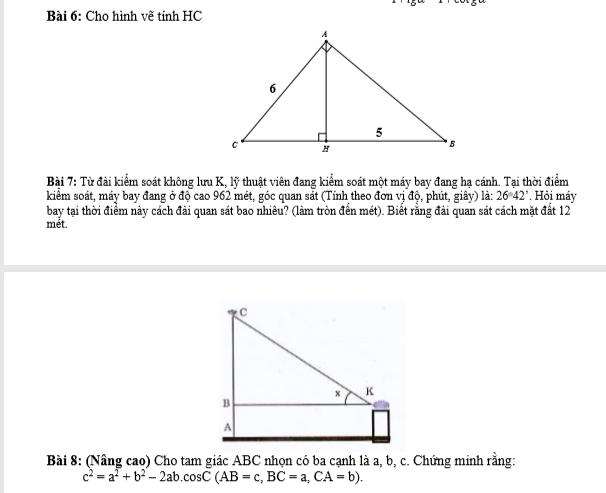
Giải giúp với ạ