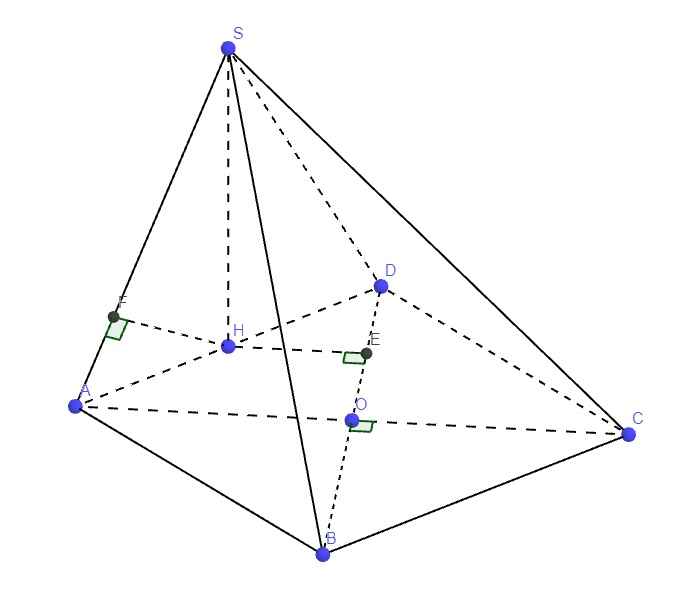
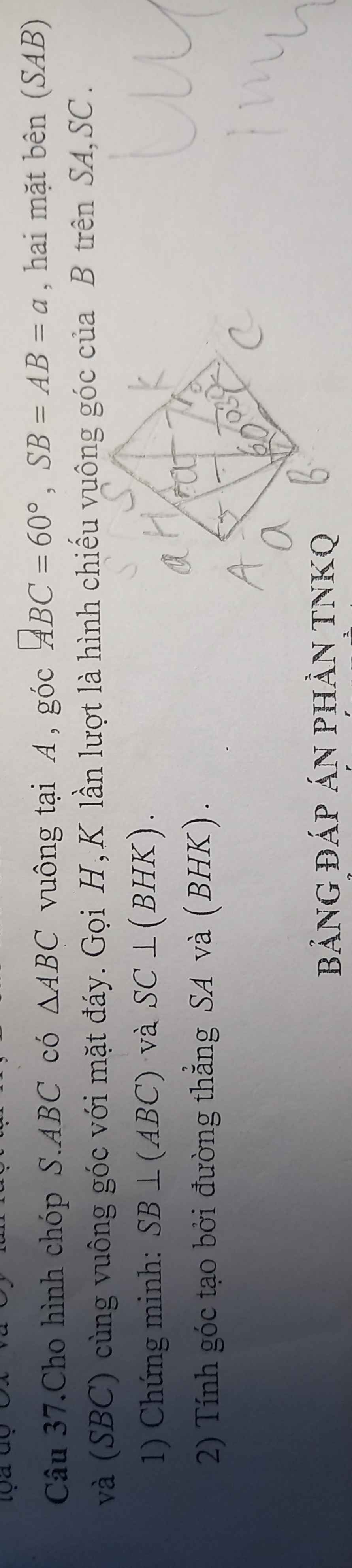a.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AB\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow AB\perp SA\Rightarrow\Delta SAB\) vuông tại A
Theo cmt \(AB\perp\left(SAD\right)\)
Mà \(AB=\left(SAB\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SAD}\) là góc giữa (SAB) và (ABCD)
Mà tam giác SAD đều theo giả thiết \(\Rightarrow\widehat{SAD}=60^0\)
b.
Gọi E là trung điểm OD \(\Rightarrow HE\) là đường trung bình tam giác ADO
\(\Rightarrow HE||AO\Rightarrow HE\perp BD\) (do \(AO\perp BD\) theo t/c hình vuông)
Lại có \(SH\perp\left(ABCD\right)\Rightarrow SH\perp HE\)
\(\Rightarrow HE\) là đường vuông góc chung của SH và BD
\(\Rightarrow d\left(SH;BD\right)=HE=\dfrac{1}{2}OA=\dfrac{1}{4}AC=\dfrac{a\sqrt{2}}{4}\)
Ý 2 của câu b bị lặp lại ý 2 của câu a?
c.
Từ H kẻ HF vuông góc SA (F thuộc SA)
Do \(AB\perp\left(SAD\right)\) (theo cm câu a) \(\Rightarrow AB\perp HF\)
\(\Rightarrow HF\perp\left(SAB\right)\Rightarrow HF=d\left(H;\left(SAB\right)\right)\)
\(SA=AD=a\) (tam giác SAD đều), \(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều); \(AH=\dfrac{AD}{2}=\dfrac{a}{2}\)
Hệ thức lượng trong tam giác vuông SAH:
\(HF=\dfrac{SH.AH}{SA}=\dfrac{a\sqrt{3}}{4}\)
Mà H là trung điểm AD, O là trung điểm BD \(\Rightarrow OH\) là đường trung bình tam giác ABD
\(\Rightarrow OH||AB\Rightarrow OH||\left(SAB\right)\Rightarrow d\left(O;\left(SAB\right)\right)=d\left(H;\left(SAB\right)\right)=\dfrac{a\sqrt{3}}{4}\)