Bài 1:
\((n+1)^n-1=n[(n+1)^{n-1}+(n+1)^{n-2}+....+(n+1)+1]\)
Giờ ta chỉ cần cmr \((n+1)^{n-1}+(n+1)^{n-2}+...+(n+1)+1\vdots n\)
Thật vậy:
\((n+1)^{n-1}+(n+2)^{n-2}+...+(n+1)+1\equiv 1^{n-1}+1^{n-2}+...+1^1+1=n\equiv 0\pmod n\)
Do đó ta có đpcm.
Bài 2 em xem lại. Số $2^{n(2^n-1)}$ chỉ toàn ước có dạng $2^k$ với $k=0,1,..., n(2^n-1)$ trong khi đó $(2^n-1)^2$ là số lẻ.










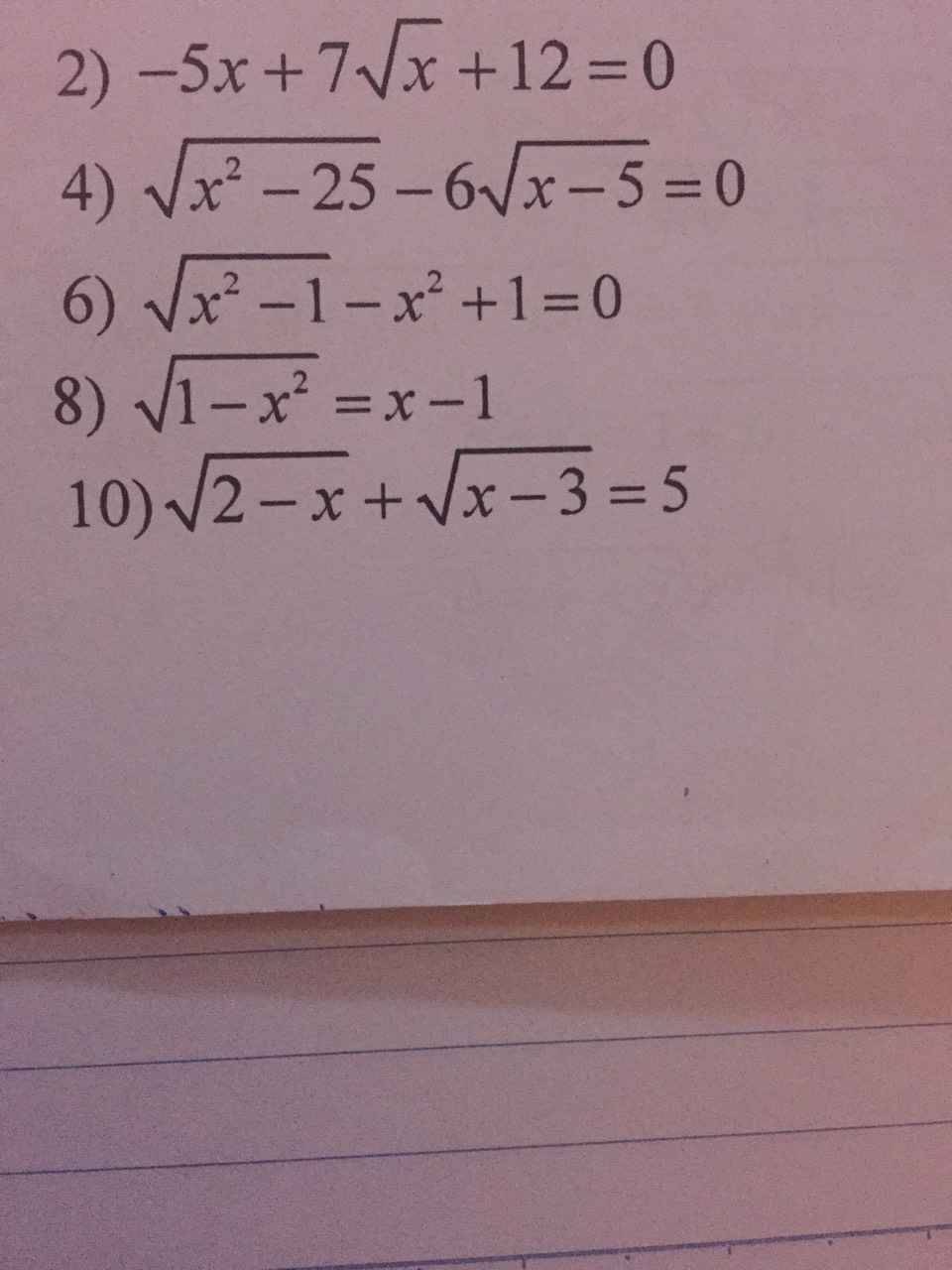
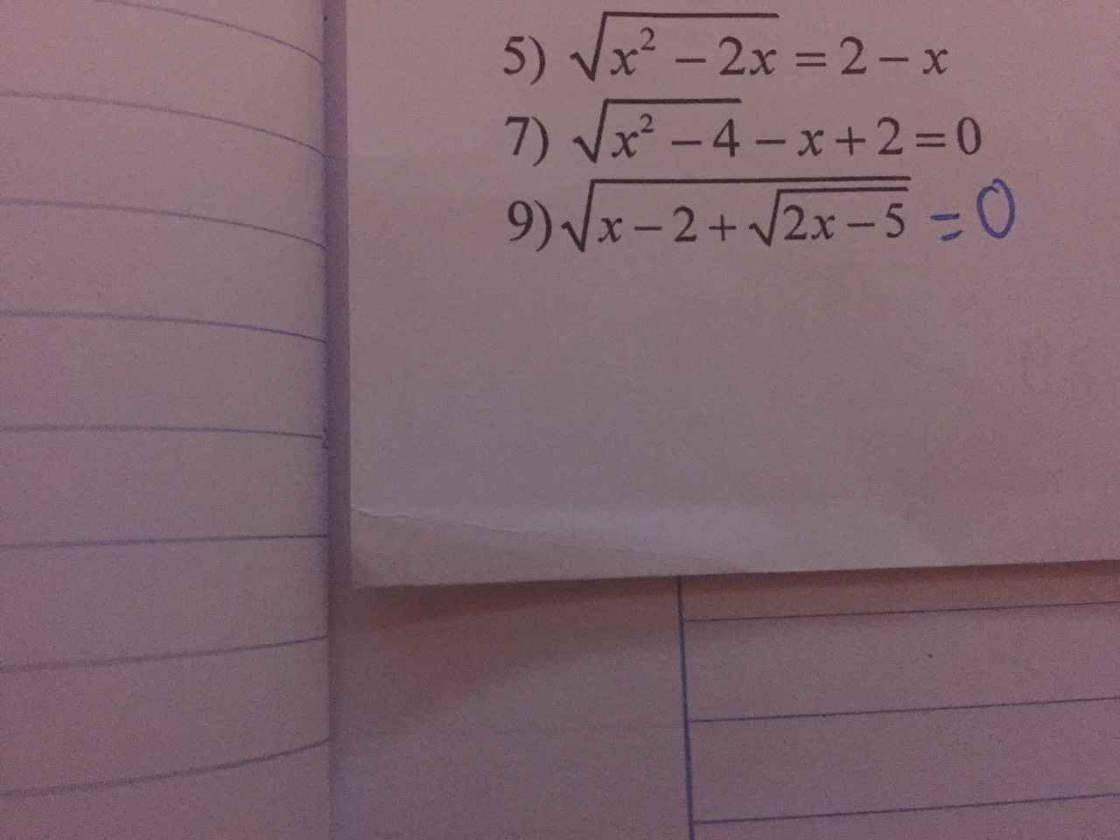 giúp với ạ! xin cảm ơn!
giúp với ạ! xin cảm ơn!