a) ta có:tg AMB =TG AMC suy ra AB= AC suy ra tg ABC cân tại A
suy ra BM=MC suy ra AM là đưòng trung tuyến tg ABC
Mà tg ABC cân tại A suy ra AM là pg góc A( tính chất tg cân)
b) suy ra AM là đưòng cao tg ABC (tính chất tg cân)
suy ra AM vuông góc BC.
Đây nè bạn!!!!
a: Ta có: ΔAMB=ΔAMC
nên \(\widehat{MAB}=\widehat{MAC}\)
hay AM là tia phân giác của \(\widehat{BAC}\)
b: Ta có: ΔAMB=ΔAMC
nên \(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
hay AM\(\perp\)BC







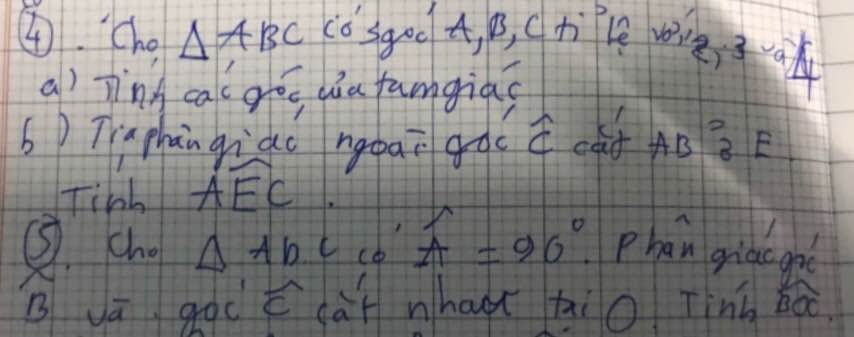
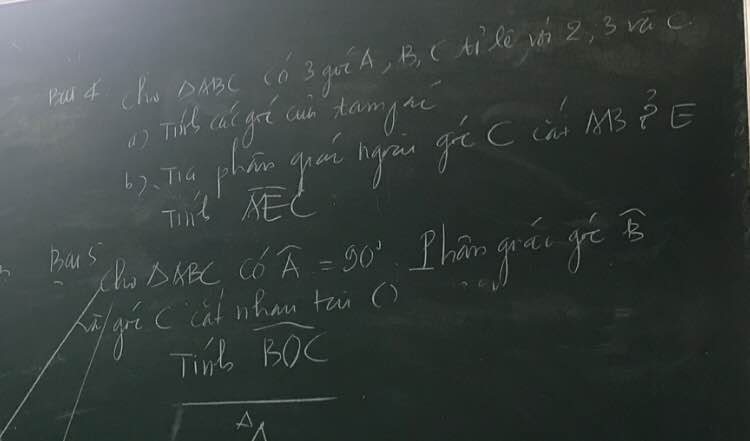








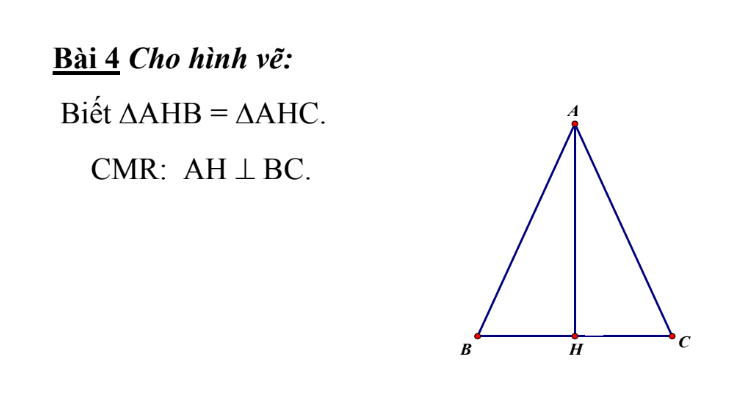 giúp mk vs, mk sẽ tick cho
giúp mk vs, mk sẽ tick cho