Ôn tập cuối năm phần hình học
Các câu hỏi tương tự
Một hình lăng trụ đứng có đáy là tam giác vuông, biết độ dài hai cạnh góc vuông của đáy là 6cm và 8cm, chiều cao của lăng trụ là 9cm. Tính diện tích toàn phần của hình lăng trụ đó.
Một mảnh đất HCN có chu vi là 46 . Nếu mở rộng mảnh đất trên thêm 1 mảnh hình vuông có cạnh đúng bằng chiều rộng của HCN thì ta được một mảnh đất mới có diện tích là 138m2 . Tính diện tích của HCN bạn đầu.
Khẳng định nào sau đây là đúng ?
A.Trong hình bình hành các góc đối bù nhau
B. Trong hình bình hành hai góc kề 1 cạnh phụ nhau
C.Trong hình chữ nhật, 2 đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường
D. Trong hình bình hành hai đường chéo = nhau
Bài 4 :Trên một cạnh của một góc có đỉnh là A, đặt đoạn thẳng AE = 3cm, AC = 8cm, trên cạnh thứ hai của góc đó đặt các đoạn thẳng AD = 4cm, AF = 6cm
a) Hai tam giác ABC và AEF có đồng dạng không? vì sao?
b) Gọi I là giao điểm của CD và EF. Tính tỉ số của 2 tam giác IDF và IEC
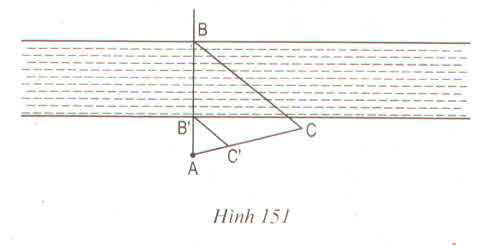
Trên hình 151 cho thấy có thể xác định chiều rộng BB' của khúc sông bằng cách xét hai tam giác đồng dạng ABC và AB'C'. Hãy tính BB' nếu AC = 100m, AC' = 32m, AB' = 34m
Cho hình thang ABCD (AB//CD). Gọi F là giao điểm của hai đường chéo AC và BD.
a, CM: ΔFAB đồng dạng với ΔFCD
b, CM: FA.FD=FB.FC
c, Đường thẳng qua F vuông góc với AB tại M và cắt CD tại N, biết FB=3cm; FD= 6cm; FM= 2cm; CD= 8cm. Hãy tính diện tích ΔFCD
Học kì I, số học sinh giỏi của lớp 8A bằng 30% số học sinh cả lớp. Sang học kì II, có thêm 4 bạn phấn đấu trở thành học sinh giỏi nữa, do đó số học sinh giỏi bằng \(\dfrac{2}{5}\) số học sinh cả lớp. Hỏi lớp 8A có bao nhiêu học sinh ?
Cho hình vuông ABCD. M là một điểm nằm trên BD (M khác B và D). Gọi E và F lần lượt là hình chiếu của M trên AB và AD.
a) ABMF là hình gì? Vì sao
b) Chứng minh DE=CF
c) Chứng minh DE, BF, CM đồng quy
MỌI NGƯỜI CHỈ CẦN TÓM TẮT CHO EM CÁCH LÀM CỦA CÂU C THÔI CŨNG ĐƯỢC Ạ. EM CẢM ƠN NHIỀU Ạ
Cho hình thang ABCD (AB//CD). Gọi I là giao điểm của hai đường chéo AC và BD. Vẽ qua I một đường thẳng song song với AB cắt AD và BC lần lượt tại E và F. CMR:a. IEIF b. dfrac{2}{EF}dfrac{1}{AB}+dfrac{1}{CD}
Đọc tiếp
Cho hình thang ABCD (AB//CD). Gọi I là giao điểm của hai đường chéo AC và BD. Vẽ qua I một đường thẳng song song với AB cắt AD và BC lần lượt tại E và F. CMR:
a. IE=IF
b. \(\dfrac{2}{EF}\)=\(\dfrac{1}{AB}\)+\(\dfrac{1}{CD}\)









