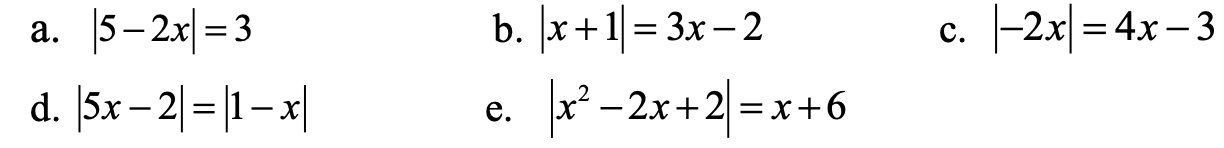d. \(\left|5x-2\right|=\left|1-x\right|\)
\(\Leftrightarrow\left(5x-2\right)^2=\left(1-x\right)^2\)
\(\Leftrightarrow\left(5x-2\right)^2-\left(1-x\right)^2=0\)
\(\Leftrightarrow\left(5x-2+1-x\right)\left(5x-2-1+x\right)=0\)
\(\Leftrightarrow\left(4x-1\right)\left(6x-3\right)=0\)
\(\Leftrightarrow4x-1=0\) hay \(6x-3=0\)
\(\Leftrightarrow x=\dfrac{1}{4}\) hay \(x=\dfrac{1}{2}\)
-Vậy \(S=\left\{\dfrac{1}{2};\dfrac{1}{4}\right\}\)
e. Vì \(x^2-2x+2=\left(x-1\right)^2+1>0\forall x\Rightarrow\left|x^2-2x+2\right|=x^2-2x+2\)
-ĐK: \(x+6\ge0\Leftrightarrow x\ge6\)
PT \(\Leftrightarrow x^2-2x+2=x+6\)
\(\Leftrightarrow x^2-2x-x+2-6=0\)
\(\Leftrightarrow x^2-3x-4=0\)
\(\Leftrightarrow x^2-4x+x-4=0\)
\(\Leftrightarrow x\left(x-4\right)+x-4=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+1\right)=0\)
\(\Leftrightarrow x-4=0\) hay \(x+1=0\)
\(\Leftrightarrow x=4 \left(nhận\right)\) hay \(x=-1\left(nhận\right)\)
-Vậy \(S=\left\{4;-1\right\}\)
a. th1: 5-2x= 3 nếu 5-2x>0 => x< \(\dfrac{5}{2}\)
5-2x= 3
-2x= -2
x=1 (chọn)
th2: 5-2x= -3 nếu 5-2x<0 => x>\(\dfrac{5}{2}\)
5-2x=-3
-2x= -8
x= 4 (chọn)
S={1,4}
b. th1: x+1 = 3x -2 nếu x+1>0 => x>-1
x+1=3x-2
x-3x= -2-1
-2x= -3
x= \(\dfrac{3}{2}\)(chọn)
th2: x+1 = -3x -2 nếu x+1<0 => x<-1
x+1=-3x-2
x+3x= -2-1
4x= -3
x= \(\dfrac{-3}{4}\)(loại)
S={\(\dfrac{3}{2}\)}