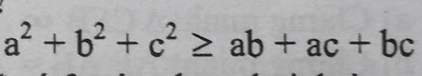Áp dụng bất đẳng thức Cô si cho các số dương \(a^2, b^2, c^2\)
\(a^2+b^2\ge 2\sqrt{a^2b^2}=2\sqrt{ab}\)
\(b^2+c^2\ge 2\sqrt{b^2c^2}=2\sqrt{bc}\)
\(a^2+c^2\ge 2\sqrt{a^2c^2}=2\sqrt{ac}\)
Cộng các vế bất đẳng thức với nhau ta được bất đẳng thức:
\(2(a^2+b^2+c^2)\ge 2(ab+bc+ac)\)
\(\to a^2+b^2+c^2\ge ab+bc+ac\)
\(\to\) Dấu "=" xảy ra khi \(\begin{cases}a^2=b^2\\b^2=c^2\\a^2=c^2\end{cases}\to a=b=c\)