Question

Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.

Ko chép giải

 

 

Answer 1

 

Cho hình chữ nhật ABCD , gọi M ; N ; P ; Q lần lượt là trung điểm của Ab ; BC ; CD ; Da .

Dễ dàng c/m được \(\Delta AMQ=\Delta BMN=\Delta DPN=\Delta CPQ\left(c.g.c\right)\)

=> QM = MN = NP = PQ ( các cạnh tương ứng )

=> Tứ giác MNPQ là hình thang

Answer 2

Bài giải:

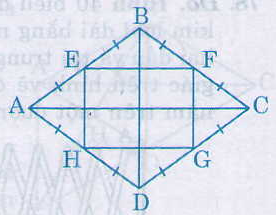
Ta có: EB = EA, FB = FA (gt)

nên EF là đường trung bình của ∆ABC.

Do đó EF // AC

HD = HA, GD = GC (gt)

nên HG là đường trung bình của ∆ADC.

Do đó HG // AC

Suy ra EF // HG (1)

Chứng minh tương tự EH // FC (2)

Từ (1) (2) ta được EFGH là hình bình hành.

Lại có EF // AC và BD ⊥ AC nên BD ⊥ EF

EH // BD và EF ⊥ BD nên EF ⊥ EH

nên = 90⁰

Hình bình hành EFGH có = 90⁰ nên là hình chữ nhật.