Bài 9: Hình chữ nhật
Các câu hỏi tương tự
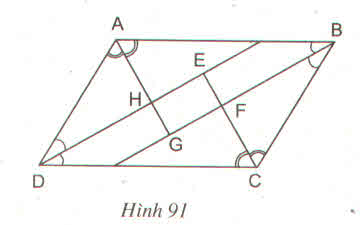
Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như hình 91. Chứng minh rằng EFGF là hình chữ nhật
Cho hình chữ nhật ABCD. Vẽ AI, CK cùng vuông góc với BD.
a) Chứng minh tam giác AID bằng tam giác CKB
b) Chứng minh tứ giác AICK là hình bình hành
c) Gọi O là trung điểm của BD, tia AI cắt BC tại M, tia CK cắt AD tại N. Chứng minh 3 điểm M,O,N thẳng hàng
Cho hình chữ nhật ABCD. Vẽ AI, CK cùng vuông góc với BD.
a) Chứng minh tam giác AID bằng tam giác CKB
b) Chứng minh tứ giác AICK là hình bình hành
c) Gọi O là trung điểm của BD, tia AI cắt BC tại M, tia CK cắt AD tại N. Chứng minh 3 điểm M,O,N thẳng hàng
HELP ME PLS
Bài 3. Cho hình chữ nhật ABCD có tia phân giác góc A đi qua trung điểm E của cạnh CD. Gọi M, N, P theo thứ tự là trung điểm của AD, AE, BC. 1. Chứng minh rằng AB = 2AD và NP = 3NM. 2. Chứng minh rằng AE ⊥ DN. 3. Chứng minh rằng tia phân giác của góc BCD, BE, MN đồng quy
Cho tứ giác ABCD . Gọi E, F,G,H lần lược là trung điểm của AB, BC, CD, AD Bé vịt nhỏ A) chứng minh rằng : tứ giác EFGH là hình bình hành b) cho AC vuông góc với BD . Chứng minh EFGH là hình chữ nhật . ( Vẽ hình , ghi giả thiết , kết luận đc 0.5 ₫
Cho tam giác ABC cân tại A. Từ một điểm D trên đáy BC, vẽ đường thẳng vuông góc với BC cắt các đường thẳng AB, AC lần lượt tại N và M. gọi H và K lần lượt là trung điểm của BC và MN. Chứng minh rằng tứ giác AKDG là hình chữ nhật
Các câu sau đúng hay sai ?
a) Hình chữ nhật là tứ giác có tất cả các góc bằng nhau
b) Tứ giác có hai đường chéo bằng nhau là hình chữ nhật
c) Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình chữ nhật
cho tam giác abc vuông tại b. m,n là trung điểm ba,bc. k là tia đối của mn sao cho mn=mk nối k với b, a với n . a) chứng minh tứ giác akbn,aknc là hình bình hành b) gọi h là hình chiếu của k xuống bc. chứng minh tứ giác akhb là hình chữ nhật c) gọi giao điểm của ah và bk là o ; giao điểm của kc và an là i . chứng minh tứ giác hoin là hình thang cân
giúp mình với mình cần gấp
Cho tam giác nhọn ABC, các đường cao BD và CE cắt nhau ở H. Gọi M là trung điểm AB.
Đường thẳng qua C và vuông góc với MD cắt BD ở K. Chứng minh rằng:
a) CA là tia phân giác của góc HCK
b) CH = CK










