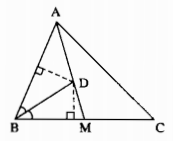
D cách đều hai cạnh của góc B nên D nằm trên đường phân giác của góc ABC
D nằm trên đường trung tuyến AM.
Vậy D là giao điểm của đường phân giác của góc ABC và đường trung tuyến AM.
Ta có hình vẽ:
Giải hộ mình bài này trong tối nay được không ạ ?
Cho tam giác ABC các trung tuyến , AM ∩ BE ∩ CF tại G , trên tia AD lấy điểm D sao cho G là trung điểm AD )
a) So sánh các cạnh của tam giác BGD với các trung tuyến của tam giác ABC
b) So sánh các trung tuyến của tam giác BGD với các cạnh của tam giác ABC
Cho tam giác cân ABC, AB = AC. Trên các cạnh AB, AC lần lượt lấy hai điểm P, Q sao cho AP = AQ. Hai đoạn thẳng Cp, BQ cắt nhau tại O. Chứng minh rằng :
a) Tam giác OBC là tam giác cân
b) Điểm O cách đều hai cạnh AB, AC
c) AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó
Cho tam giác ABC nhọn (AB<AC). AM là đường phân giác của đỉnh A, trên cạnh AC lấy điểm D sao cho AD=AB, tia AB cắt tia DM tại E. Chứng minh tam giác CME cân
Cho tam giác ABC, có góc B+ góc C= 60 độ, phân giác AD. Trên AD lấy điểm O. Trên tia đối của tia AC lấy điểm M sao cho góc ABM= góc ABO. Trên tia đối của AB lấy điểm N sao cho góc ACN= góc ACO. CMR:
a, AM=AN
b, Tam giác MON đều
Cho tam giác ABC=90 độ và AB<AC. Trên cạnh AC lấy điểm D sao cho AD=AB. Trên tia đối của tia AB lấy điểm E sao cho AE=AC. a. CM DE=BC b. CM DE vuông góc vs BC c. Biết 4. góc B=5.Góc . Tính góc AED.
Cho tam giác ABC có 3 góc đều nhọn và AH là đường cao. Trên nữa mặt phẳng bờ BC, vẽ các tia HI và HF theo thứ tự vuông góc với các cạnh AC và AB ( I thuộc AC , F thuộc AB) . Trên tia HI lấy điểm E và trên tia HF lấy điểm D sao cho I là trung điểm HE , F là trung điểm HD.
a) Chứng minh : tam giác AFD = tam giác AFH .
b) So Sánh độ dài hai cạnh AD và AE
c) DE cắt AB Và AC lần lượt tại M và N. Chứng minh HA là tia phân giác của góc MHN
Giúp en với mai e KT 1 tiết r
Cho góc đỉnh O khác góc bẹt
a) Từ một điểm M trên tia phân giác của góc O, kẻ các đường vuông góc MA, MB đến hai cạnh của góc này. Chứng minh rằng \(AB\perp OM\)
b) Trên hai cạnh của góc O lấy hai điểm C và D, sao cho OC = OD. Hai đường thẳng lần lượt vuông góc với hai cạnh của góc O tại C và D cắt nhau ở E. Chứng minh OE là tia phân giác của góc O.
Cho tam giác ABC đều vẽ tam giác ADC ở ngoài tam giác ABC sao cho góc ADC = 120 độ a, CMR: DA+DC=DB b, CMR: DB là phân giác của tam giác ADC
