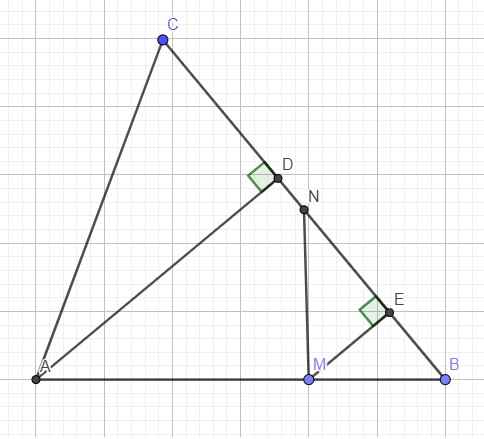
N là trung điểm BC \(\Rightarrow BN=\dfrac{1}{2}BC\)
Kẻ đường cao AD và ME ứng với BC
Do AD và ME cùng vuông góc BC \(\Rightarrow AD||ME\)
Áp dụng định lý Talet:
\(\dfrac{ME}{AD}=\dfrac{BM}{BA}=\dfrac{1}{3}\Rightarrow ME=\dfrac{1}{3}AD\)
Ta có:
\(\dfrac{S_{BMN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}.ME.BN}{\dfrac{1}{2}AD.BC}=\dfrac{\dfrac{1}{3}AD.\dfrac{1}{2}BC}{AD.BC}=\dfrac{1}{6}\)
Cho tam giác ABC, M là trung điểm của cạnh AB, N thuộc cạnh AC sao cho SAMN =\(\dfrac{1}{8}SABC\). Tính tỉ số \(\dfrac{AN}{AC}\)
Cho tam giác ABC có AB>AC. Trên cạnh AB lấy điểm M sao cho AM=\(\dfrac{1}{3}\)AB, trên AC lấy điểm N sao cho AN=\(\dfrac{1}{3}\) AC. Gọi O là giao điểm của BM và CN, F là giao điểm của AO và BC, vẽ AI \(\perp\)BC tại I, OG \(\perp\) BC tại G, BD \(\perp\) FA tại D, CE \(\perp\) FA tại E. So sánh CA với BD, OG với IA, OA với FO?
1. tam giác ABC, \(\widehat{A}>90^o,AB< AC\),đường cao AH.Về phía trong góc BAC dựng D,E sao cho AD⊥AB,AD=AB ;AE⊥AC,AE=AC. M là trung điểm của DE. Cmr : A,H,M thẳng hàng
2. ΔABC. Trên các cạnh BC,CA,AB lần lượt lấy M,N,P sao cho \(\dfrac{BM}{BC}=\dfrac{CN}{CA}=\dfrac{AP}{AB}=k\left(k>0\right)\) . Dựng hình bình hành ABCD , lấy Q ∈CD sao cho CQ=AP
a) Cmr : AM, BN, CP là độ dài 3 cạnh của 1 Δ
b) Tìm k để diện tích ΔAMQ max
Cho tam giác ABC. Trên cạnh Ab, AC lần lượt lấy hai điểm M và N sao cho AM=\(\dfrac{2}{3}\).BM; AN=\(\dfrac{3}{2}\).NC. Gọi O là giảo điểm của BN và CM. Chứng minh: SBOC=2.SAMON.
Cho tam giác ABC có M,N lần lượt là trung điểm của BC và AB a) cm diện tích tam giác ABM bằng diện tích tam giác ACM. b)tính Sbmn/Sabc
Cho tam giác ABC; M, N là trung điểm của AC và AB; ND//BM (D thuộc BC); diện tích ABC=a(cm2)
a) Tính diện tích CMND
b) a=128 (cm2); BC=32 (cm). Tính chiều cao của hình thang CMND
Cho tam giác abc. Trên cạnh bc lấy điểm m sao cho bm=3/4 bc. Chứng minh rằng S abm =3/4 S abc
Cho tam giác ABC, trên cạnh AB lấy điểm M sao cho AM=1313AB, trên cạnh AC lấy điểm N sao cho AN=1313AC. Gọi O là giao điểm của BN và CM
a) CM: diện tích tam giác BOC = 2 lần diện tích tam giác BOA
b)Từ diểm C và B hạ BD vuông góc OA. CM:BD=CE
c)Giả sử diện tích tam giác ABC= a (đơn vị diện tích). Tính diện tích AMON
Cho tam giác ABC, I là một điểm nằm trong tam giác. IA, IB, IC theo thứ tự cắt BC, CA, AB tại M, N, P. Chứng minh \(\dfrac{MB}{MC}.\dfrac{NC}{NA}.\dfrac{PA}{PB}=1\)
