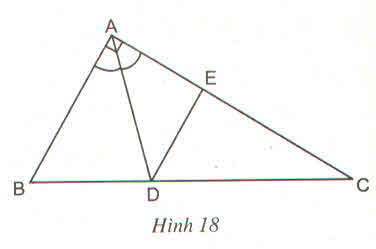
Gọi O là giao điểm của AC và BD
Xét ΔAEO và ΔCBO có
\(\widehat{AOE}=\widehat{COB}\)(hai góc đối đỉnh)
\(\widehat{AEO}=\widehat{CBO}\)(hai góc so le trong, AE//BC)
Do đó: ΔAEO\(\sim\)ΔCBO(g-g)
\(\Leftrightarrow\dfrac{OE}{OB}=\dfrac{OA}{OC}\)(Các cặp cạnh tương ứng)
hay \(\dfrac{OE}{OA}=\dfrac{OB}{OC}\)(1)
Xét ΔBOF và ΔDOA có
\(\widehat{BOF}=\widehat{DOA}\)(hai góc đối đỉnh)
\(\widehat{BFO}=\widehat{DAO}\)(hai góc so le trong, BF//AD)
Do đó: ΔBOF\(\sim\)ΔDOA(g-g)
\(\Rightarrow\dfrac{OF}{OA}=\dfrac{OB}{OD}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{OF}{OB}=\dfrac{OA}{OD}\)
hay \(\dfrac{OB}{OF}=\dfrac{OD}{OA}\)
Ta có: \(\dfrac{OE}{OA}=\dfrac{OB}{OC}\)(cmt)
\(\dfrac{OB}{OF}=\dfrac{OD}{OA}\)(cmt)
Do đó: \(\dfrac{OE}{OA}\cdot\dfrac{OB}{OF}=\dfrac{OB}{OC}\cdot\dfrac{OD}{OA}\)
\(\Leftrightarrow\dfrac{OE\cdot OB}{OA\cdot OF}=\dfrac{OB\cdot OD}{OC\cdot OA}\)
\(\Leftrightarrow\dfrac{OE}{OF}\cdot\dfrac{OB}{OA}=\dfrac{OB}{OA}\cdot\dfrac{OD}{OC}\)
\(\Leftrightarrow\dfrac{OE}{OF}=\dfrac{OD}{OC}\)
hay \(\dfrac{OE}{OD}=\dfrac{OF}{OC}\)
Xét ΔODC có
E\(\in\)OD(gt)
F\(\in\)OC(gt)
\(\dfrac{OE}{OD}=\dfrac{OF}{OC}\)(cmt)
Do đó: EF//DC(Định lí Ta lét đảo)