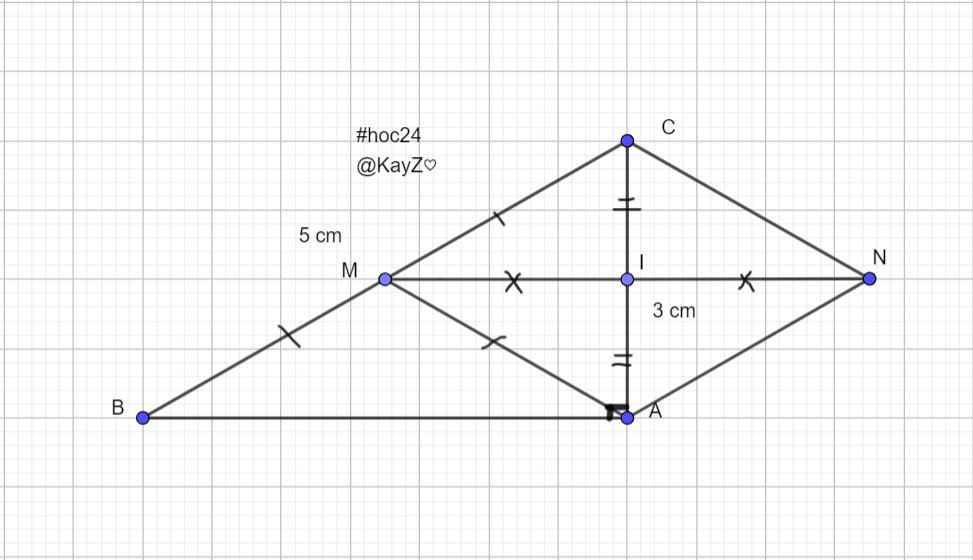
`a)`Vì `M` là trung điểm của `BC`
`=>MA` là đường trung tuyến của `ΔABC⊥` tại `A`
`=>AM=MB=MC=BC/2`
`=>AM=5/2=2,5cm`
`-` mặc khác:`M` là trung điểm của `BC`
`I` là trung điểm cuả `AC`
`=>MI` là đường trung bình của `ΔABC`
`=>MI=AB/2`
`@ΔABC` vuông tại `A`
`=>AB=`\(\sqrt{BC^2-AC^2}=\sqrt{5^2-3^2}=4cm\)
`=>MI=AB/2 = 4/2 =2cm`
`b)` Ta có:Xét `ΔMCI` và `ΔNAI` có:
`MI=IN`(Vì `N` đối xứng với `M` )
`CI=IA`(gt)
\(\widehat{MIC}=\widehat{NIA}\)(2 góc đối đỉnh)
`=>ΔMCI=ΔNAI(c.g.c)`
`=>MC=AN`(2 cạnh tương ứng) `(1✰)`
Xét `ΔMIA` và `ΔNIC` có:
`MI=IN`(Vì `N` đối xứng với `M` )
`CI=IA`(gt)
\(\widehat{MIA}=\widehat{NIC}\)(2 góc đối đỉnh)
`=>ΔMIA=ΔNIC(c.g.c)`
`=>MA=NC`(2 cạnh tương ứng) `(2✰)`
`@` Từ `(1✰)` và `(2✰)=>` tứ giác `MCNA` là hình bình hành
mà `MA=MC`(theo `a`)
`=>`tứ giác `MCNA` là hình thoi `(đpcm)`













