Question

Cho tam giác ABC vuông tại A , đường cao AH, AH=8, BH=6. Tính AB, AC?

 

 

A. 

AB=10; AC=9/1600

 

B. 

AB=10; AC=40/3

 

C. 

AB=10; AC=3/40

 

D. 

AB=9; AC=40/3

Answer 1

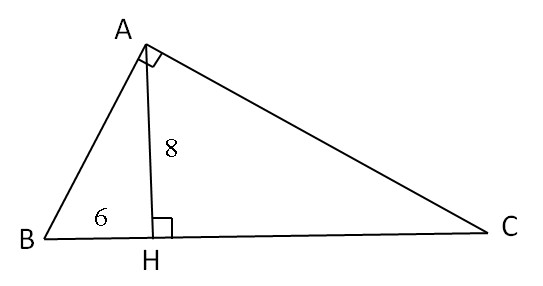
\(HC=\dfrac{8^2}{6}=\dfrac{64}{6}=\dfrac{32}{3}\left(cm\right)\)

BC=32/3+6=32/3+18/3=50/3(cm)

\(AB=\sqrt{6\cdot\dfrac{50}{3}}=10\left(cm\right)\)

\(AC=\sqrt{\dfrac{32}{3}\cdot\dfrac{50}{3}}=\dfrac{40}{3}\left(cm\right)\)

Answer 2

Áp dụng định lí Pitago cho tam giác \(BHA\) vuông tại H, ta có:

\(BH^2+HA^2=AB^2\Rightarrow AB=\sqrt{6^2+8^2}=\sqrt{100}=10\)

Ta có: \(tg\widehat{ABH}=\dfrac{BH}{AB}=\dfrac{6}{10}\Rightarrow\widehat{ABH}=30^{\circ}57'\)

Nhận thấy \(\widehat{BAH}=\widehat{BCA}\Rightarrow AC=ABtg\widehat{BCA}=\dfrac{10AB}{6}=\dfrac{50}{3}\).