a: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(BH=\dfrac{3^2}{5}=1.8\left(cm\right)\)
CH=5-1,8=3,2(cm)
\(AH=\sqrt{1.8\cdot3.2}=2.4\left(cm\right)\)
b: \(AE\cdot EB+AF\cdot FC\)
\(=HE^2+HF^2=FE^2=HA^2\)
Cho tam giác ABC vuông tại A có đường cao AH.
1) Cho biết AB=3 cm, AC=4 cm. Tính độ dài các đoạn BC,HB,HC,AH
2) Vẽ HE vuông góc với AB tại E, HF vuông góc với AC tại F
a) Chứng minh: AE.EB=HE2
b) Chứng minh: AE.EB+AF.FC=AH2
3) Chứng minh: BE=BC. cos3 B
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ HE vuông góc với AB tại E, HF vuông góc với AC tại F.
a) Cho biết AB = 3cm, AC = 4cm. Tính độ dài các đoạn HB, HC, AH
b) Chứng minh: AE.EB + AF.FC = AH2
c) Chứng minh: BE = BC.cos3B
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ HE vuông góc với AB tại E, HF vuông góc với AC tại F.
a) Cho biết AB = 3cm, AC = 4cm. Tính độ dài các đoạn HB, HC, AH
b) Chứng minh: AE.EB + AF.FC = AH2
c) Chứng minh: BE = BC.cos3B
Cho tam giác ABC vuông tại A, có đường cao AH. Vẽ HE vuông góc AB tại E ; vẽ HF vuông góc AC tại F.
Chứng minh: AE.AB=AF.AC
Chứng minh: HB/HC = (AB/AC)2
Bài 3: Cho ∆ ABC vuông tại A, đường cao AH biết HB=4cm ; HC= 9cm . a) Tính AB và AH. b) Từ HE vuông góc với AB, HF vuông góc với AC Tử giác AEHF là hình gì? Tính EF ?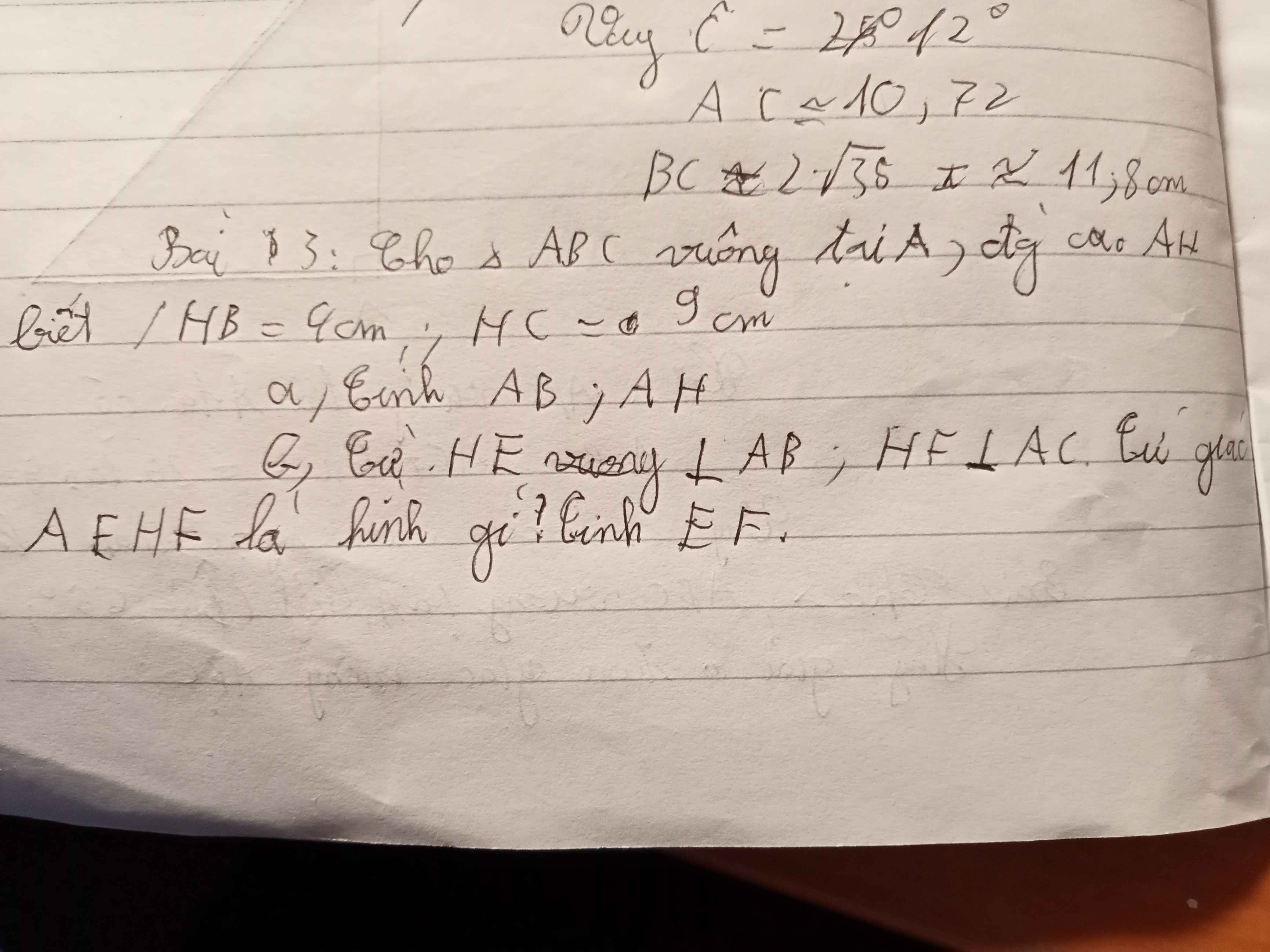
Cho tam giác ABC vuông tại A, đường cao AH (HϵBC)
a) Biết AB = 12cm, BC = 20cm. Tính AC, B, AH (góc làm tròn đến độ)
b) Kẻ HE vuông góc AB (EϵAB). Chứng minh: AE.AB=AC2-HC2
c) Kẻ HF vuông góc AC (FϵAC). Chứng minh: AF=AE.tanC
Cho tam giác ABC vuông tại A, (AB<AC) đường cao AH. Trung tuyến AM, từ H kẻ HE vuông góc AB, HF vuông góc AC (E thuộc AB, F thuộc AC). Gọi O là giao điểm của AH và EF. Chứng minh: a. AH^2=AE.EB+AF.FC b.AH^3=BC.HE.HF c. AB^2/AC^2=HB/HC d.AH=BC.sinB.cosC e.HB=BC.cos^2.B f.HC=BC.sin^2.B
Cho tam giác ABC vuông tại A, có đường cao AH. Vẽ HE vuông góc AB tại E ; vẽ HF vuông góc AC tại F. Chứng minh: (AE.AB)/(EF.BC) = AF/AB
Cho tam giác abc, đường cao ah kẻ hm,hn lần lượt vuông góc với ab và ac a, chứng minh mb/nh = ab mũ 2 / ac mũ 2 b, chứng minh bc.bm.cn=ah mũ 3 c, chứng minh am.ab=hb.hc=mn mũ 2 d, chứng minh bm.ba+an.ac=hb.bc e, cho hb=4cm, hc=9cm tính chu vi tam giác abc và diện tích tứ giác amhn f, gọi m,n lần lượt là hình chiếu cửa h trên ab,ac chứng minh ah mũ 3 =am.an.bc g, chứng minh (ab/ac) mũ 3 = bm/cn h, chứng minh căn bậc 3 bc mũ 2 = căn bậc 3 bm mũ 2 + căn bậc 3 cn mũ 2 i, chứng minh bm.ba+cn.ca+2.bh.ch=bc mũ 2
Cho tam giác ABC vuông tại A, đường cao AH, AB=3cm, BC=6cm. 1) Giải tam giác ABC 2) Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC. a) Tính độ dài AH và chứng minh: EF=AH b) Tính: EA.EB+AF.FC
