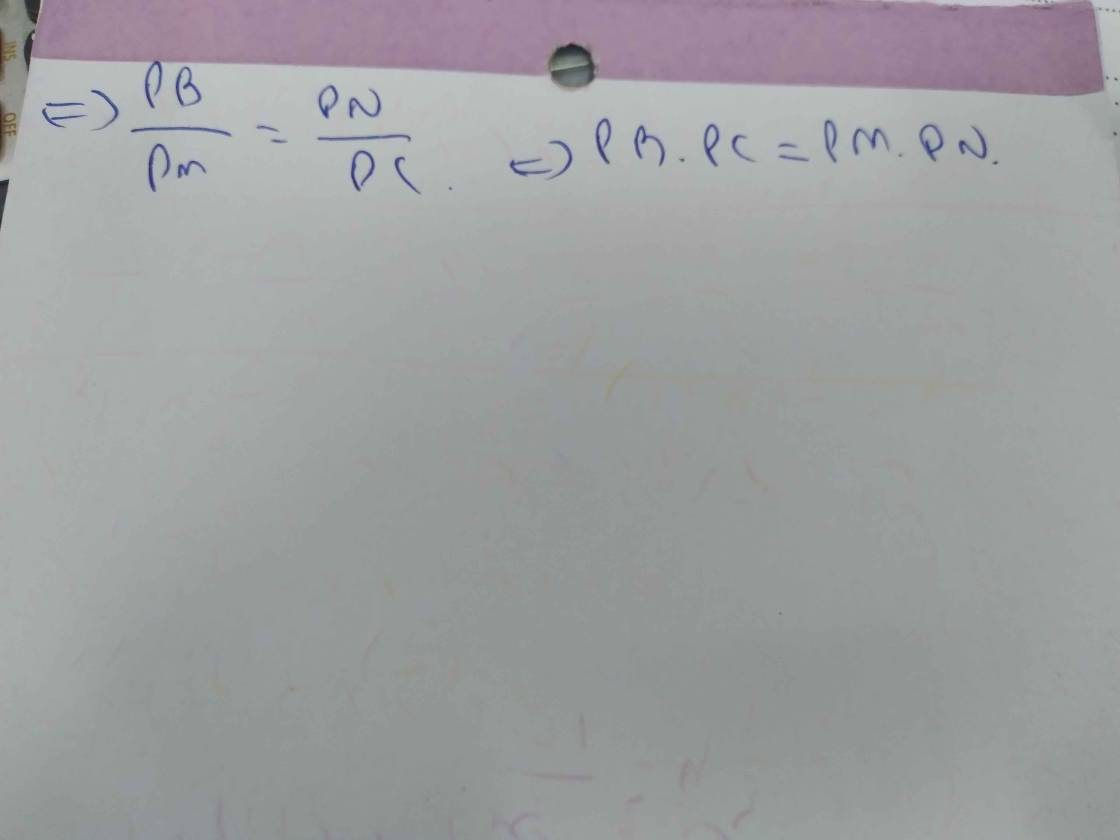Ôn thi vào 10
Các câu hỏi tương tự
bài 8/77
cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn ,các đường cao AI < BK của tam giác ABC cắt nhau tại H ( I thuộc BC , K thuộc AC ) .AI vad BK cắt đường tròn O lần lượt tại D và E
A/chứng minh tứ giác ABIK nội tiếp
B/ gọi M là trung điểm của DE . chứng minh 3 điểm O,M,C thẳng hàng
C/chứng mình IK song song ED
thankkkkk
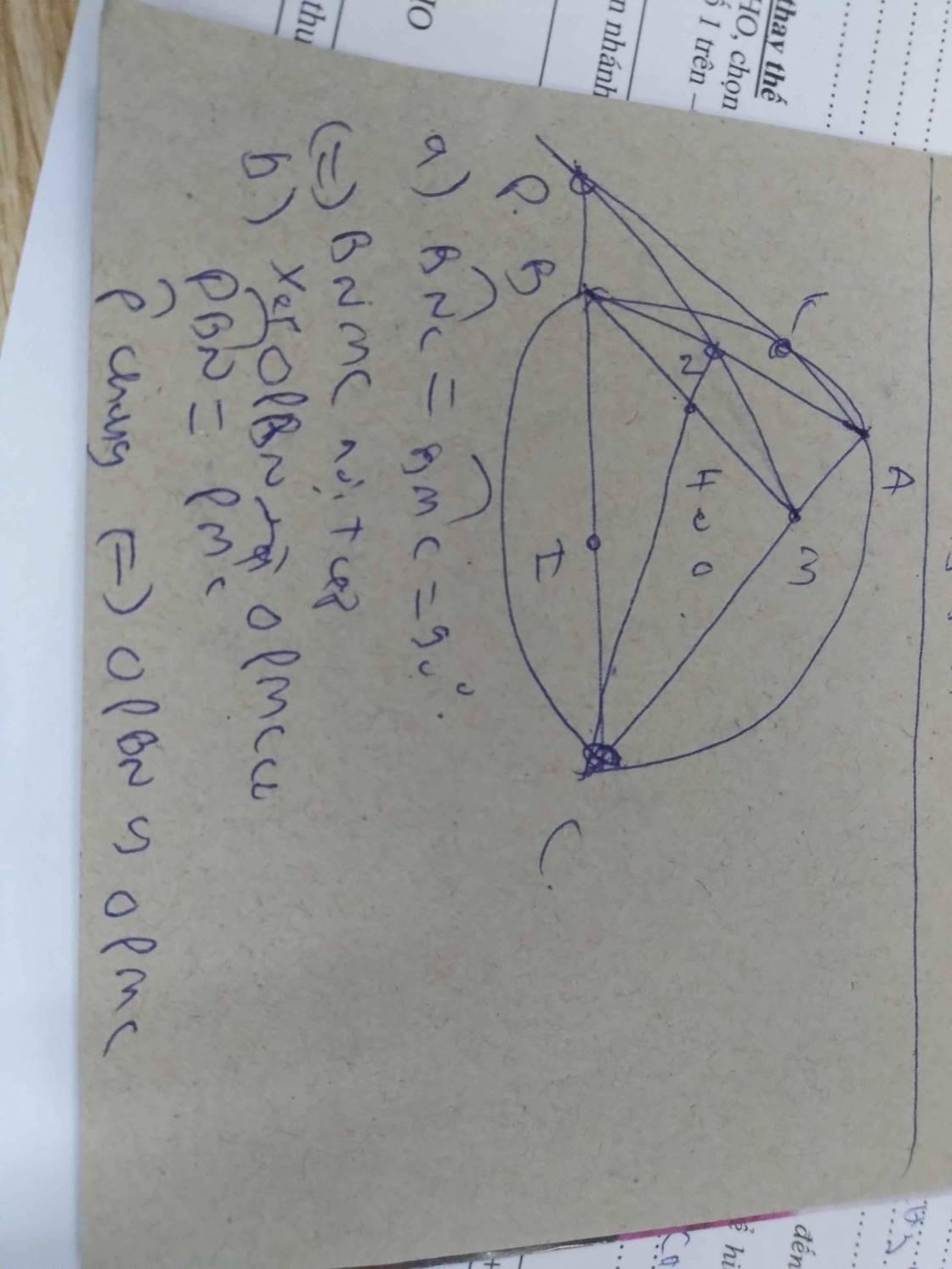
Cho tam giác ABC có 3 góc nhọn, AB AC và nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K( K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M.a) Chứng minh tứ giác ACDF nội tiếpb) AM cắt đường tròn (O) tại I( I khác A). Chứng minh MC2 MI. MA và tam giác CMD cân.c) MD cắt BI tại N. Chứng minh 3 điểm C, K, N thẳng hàng.Giúp mình với ạ
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn, AB < AC và nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K( K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M.
a) Chứng minh tứ giác ACDF nội tiếp
b) AM cắt đường tròn (O) tại I( I khác A). Chứng minh MC2 = MI. MA và tam giác CMD cân.
c) MD cắt BI tại N. Chứng minh 3 điểm C, K, N thẳng hàng.
Giúp mình với ạ
Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O). Các đường cao AD,BE,CF của tam giác ABC cắt nhau tại H
a) Chứng minh tứ giác BCEF nội tiếp
b) Gọi I là trung điểm của cạnh BC, K là điểm đối xứng của H qua I. Chứng minh ba điểm A,O,K thẳng hàng
Ai giải giúp mình câu b được không. Mình xin cảm ơn rất nhiều
Câu 4. (3,0 điểm) Cho tam giác ABC nhọn nội tiếp (O), hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Vẽ DK vuông góc với AB (K thuộc AB), gọi F là trung điểm của ED, tia BF cắt (O) tại I (khác B), a) Chứng minh tứ giác BEDC nội tiếp b) Chứng minh rằng BK.BA BF.BI c) Chứng minh rằng, hai đường thẳng AH và ID cắt nhau tại một điểm nằm trên (O).
Đọc tiếp
Câu 4. (3,0 điểm) Cho tam giác ABC nhọn nội tiếp (O), hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Vẽ DK vuông góc với AB (K thuộc AB), gọi F là trung điểm của ED, tia BF cắt (O) tại I (khác B),
a) Chứng minh tứ giác BEDC nội tiếp
b) Chứng minh rằng BK.BA = BF.BI
c) Chứng minh rằng, hai đường thẳng AH và ID cắt nhau tại một điểm nằm trên (O).
Cho tam giác ABC nhọn (AB AC) nội tiếp đường tròn (O;R) .Hai đường tròn AD và BE cắt nhau tại H. Vẽ đường kính của (O) cắt BC tại I. Gọi F là hình chiếu của C trên AB a Chứng minh tứ giác ADFC nội tiếpb Chứng minh AB . AC 2R . AD c CM: DF//CHd Vẽ đường tròn đường kính AH cắt (O) tại K. Chứng minh HK đi qua trung điểm của BC
Đọc tiếp
Cho tam giác ABC nhọn (AB > AC) nội tiếp đường tròn (O;R) .Hai đường tròn AD và BE cắt nhau tại H. Vẽ đường kính của (O) cắt BC tại I. Gọi F là hình chiếu của C trên AB
a Chứng minh tứ giác ADFC nội tiếp
b Chứng minh AB . AC = 2R . AD
c CM: DF//CH
d Vẽ đường tròn đường kính AH cắt (O) tại K. Chứng minh HK đi qua trung điểm của BC
Cho tam giác nhọn ABC nội tiếp đường tròn (O) có AB AC, các đường cao BE, CF của tam giác ABC cắt nhau tại H, đường thẳng EF cắt đường thẳng BC tại K.1. Chứng minh tứ giác BCEF nội tiếp.2. Chứng minh hai tam giác KBF và KEC đồng dạng, từ đó suy ra KB.KC KF.KE.3. Đường thẳng AK cắt lại đường tròn (O) tại G khác 4, chứng minh các điểm A, G, F, E. H củng thuộc một đường tròn.4. Gọi I là trung điểm cạnh BC, chứng minh HI vuông góc với AK.
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn (O) có AB < AC, các đường cao BE, CF của tam giác ABC cắt nhau tại H, đường thẳng EF cắt đường thẳng BC tại K.
1. Chứng minh tứ giác BCEF nội tiếp.
2. Chứng minh hai tam giác KBF và KEC đồng dạng, từ đó suy ra KB.KC = KF.KE.
3. Đường thẳng AK cắt lại đường tròn (O) tại G khác 4, chứng minh các điểm A, G, F, E. H củng thuộc một đường tròn.
4. Gọi I là trung điểm cạnh BC, chứng minh HI vuông góc với AK.
Cho tam giác ABC (AB<AC) nội tiếp đường tròn O ,2 đường cao BE và CF cắt nhau tại H
a) chứng minh : các tứ giác BCEF , tứ giác AEHF nội tiếp
b) tia BE,CF cắt đường tròn theo thứ tự tại MN . chứng minh MN song song EF
c) Gọi K là giao điểm OA và MN . chứng minh tứ giác HEKF là hình bình hành
cho tam giác ABC nhọn (AB<AC) nội tiếp (O) các đường cao AD,BE CF cắt nhau tại H
a) chứng minh CDHE nội tiếp
b) EF và BC cắt nhau tại M , chứng minh MB.MC=ME.MF
c) đường thẳng qua B và song song AC cắt AM,AH tại I,K. Chứng minh HB là phân giác của IHK
Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R) , 2 đường cao BD và CE cắt nhau tại H, gọi K là giao điểm của AO với (O;R) 1) Chứng minh: tứ giác BEDC nội tiếp2) Chứng minh: góc ABC góc ADE 3) Gọi M là trung điểm của BC. Chứng minh: 3 điểm H, M, K thẳng hàng4) Giả sử góc ACB 60 độ. Chứng minh tam giác HOC cân5) Khoảng cách từ A đến H gấp 2 lần khoảng cách từ O đến BC6) Gọi G là trọng tâm của tam giác ABC. Chứng minh: 3 điểm H,G,O thẳng hàng và HG 2GO7) AH cắt (O) tại F. Chứng minh: H và F đối xứ...
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R) , 2 đường cao BD và CE cắt nhau tại H, gọi K là giao điểm của AO với (O;R)
1) Chứng minh: tứ giác BEDC nội tiếp
2) Chứng minh: góc ABC= góc ADE
3) Gọi M là trung điểm của BC. Chứng minh: 3 điểm H, M, K thẳng hàng
4) Giả sử góc ACB = 60 độ. Chứng minh tam giác HOC cân
5) Khoảng cách từ A đến H gấp 2 lần khoảng cách từ O đến BC
6) Gọi G là trọng tâm của tam giác ABC. Chứng minh: 3 điểm H,G,O thẳng hàng và HG = 2GO
7) AH cắt (O) tại F. Chứng minh: H và F đối xứng nhau qua BC
8) Chứng minh: tứ giác BCKF là hình thang cân
9) Gọi P và Q theo thứ tự là giao điểm của BD và CE với (O). Chứng minh: PQ song song với DE
Giúp mình với T-T