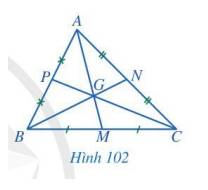
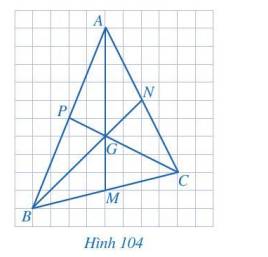
a) G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC.
Suy ra: \(AG = 2GM\). Mà trên tia đối của tia MA lấy điểm D sao cho MD = MG nên \(GD = 2GM\).
Vậy GA = GD (= 2GM).
b) Xét hai tam giác MBG và MCD có:
MB = MC (M là trung điểm cạnh BC)
\(\widehat {GMB} = \widehat {DMC}\)(đối đỉnh)
GM = GD.
Vậy \(\Delta MBG = \Delta MCD\)(c.g.c).
c) \(\Delta MBG = \Delta MCD\) nên BG = CD (2 cạnh tương ứng).
Mà G là trọng tâm tam giác ABC nên \(BG = 2GN\). Mà BG = CD nên \(CD = 2GN\).