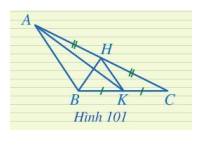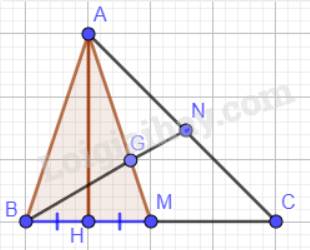
a) Xét tam giác AHB và tam giác AHM có:
AH chung;
\(\widehat {AHB} = \widehat {AHM}\)(H là hình chiếu của A lên BC nên \(AH \bot BC\));
HB = HM (H là trung điểm của BM).
Vậy \(\Delta AHB = \Delta AHM\)(c.g.c).
b) \(\Delta AHB = \Delta AHM\)nên AB = AM ( 2 cạnh tương ứng).
G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC. Nên: \(AG = \dfrac{2}{3}AM\).
Mà AB = AM suy ra: \(AG = \dfrac{2}{3}AB\).