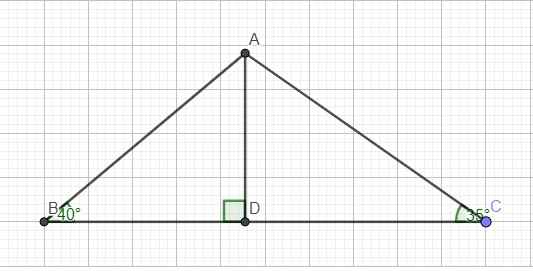
Kẻ đường cao AD ứng với BC
Trong tam giác vuông ABD:
\(cotB=\dfrac{BD}{AD}\Rightarrow BD=AD.cotB\)
Trong tam giác vuông ACD:
\(cotC=\dfrac{CD}{AD}\Rightarrow CD=AD.cotC\)
\(\Rightarrow BD+CD=AD.cotB+AD.cotC\)
\(\Rightarrow BC=AD\left(cotB+cotC\right)\)
\(\Rightarrow AD=\dfrac{BC}{cotB+cotC}\)
Trong tam giác vuông ACD:
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{BC}{sinC\left(cotB+cotC\right)}=\dfrac{20}{sin35^0\left(cot40^0+cot35^0\right)}=13,3\left(cm\right)\)
Đúng 2
Bình luận (0)
