Bài 2: Định lý đảo và hệ quả của định lý Talet
Các câu hỏi tương tự
Cho tam giác ABC có đường trung tuyến AM.Điểm D thuộc đoạn thẳng BM.Từ D kẻ tia song song với AM và cắt AB, AC lần lượt tại Evà F.Chứng minh: DE+DF=2 MA
Cho tam giác ABC, AM là đường trung tuyến, đường thẳng song song BC, cắt AB,AM,AC lần lượt ở D,N,E.
a) So sánh: DN/BM=AN/AM
NE/MC=AN/AM
b)Cm: N là trung điểm DE
Cho tam giác ABC,trung tuyến AM,D thuộc AB,từ D kẻ đường thẳng song song với BC cắt AM,AC thứ tự tại K và E.
a)CM:K là trung điểm của DE
b)CHO AK=3AM,AB=6cm,BC=9cm.Tính AD.DK
Bài 1: cho G là trọng tâm của tam giác ABC.Qua G vẽ các đường thẳng song song vs AB,AC ,cat B,C lần lượt tại D,E.CMR:
a)BD/BC=1/3
b)BD=DE=EC
Cho tam giác ABC có AB = 18 cm, AC = 12 cm, BC = 9 cm. Trên tia đối của tia CB lấy điểm D sao cho CD = 3 cm. Qua D kẻ đường thẳng song song với AB cắt tia AC tại E. Gọi F là giao điểm của AD và BE. Tính: a) Độ dài CE, DE
Cho tam giác ABC có cạnh BC = a. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M, N (h.5).
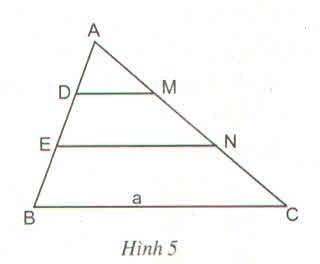
Tính theo a độ dài của các đoạn thẳng DM và EN ?
Cho tam giác ABC,các tia phân giác của các góc AMB,AMC cắt AB,AC lần lượt D,E
a)cm DE//BC
b)cho BC=6CM,AM=5CM.TÍNH DE
c) gọi I là giao điểm AM và DE nếu tam giác ABC CÓ BC CỐ ĐỊNH,AM KHÔNG ĐỔI THÌ I CHUYỂN ĐỘNG TRÊN ĐƯỜNG NÀO
Xem chi tiết
Cho DABC vuông tại A, đường phân giác của góc A cắt BC tại D biết AB = 6 cm , AC = 8 cm . a) Tính BC, BD, DC b) Từ trung điểm M của BC kẻ 1 đường thẳng song song với AD cắt cạnh AC tại F và cắt tia đối của tia AB tại E .Chứng minh: . c) Chứng minh: AE = AF









