Tham khảo:
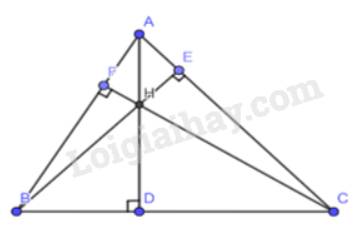
+) Xét tam giác HBC ta có :
HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC
BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC
CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC
Ta kéo dài HD, BF, CE sẽ cắt nhau tại A
\( \Rightarrow \) A là trực tâm tam giác HBC
+) Xét tam giác HAB ta có :
HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB
BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB
BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB
Ta kéo dài HF, BD, AE sẽ cắt nhau tại C
\( \Rightarrow \) C là trực tâm tam giác HAB
+) Xét tam giác HAC ta có :
HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC
AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC
CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC
Ta kéo dài CD, HE, AF sẽ cắt nhau tại B
\( \Rightarrow \) B là trực tâm tam giác HAC.



