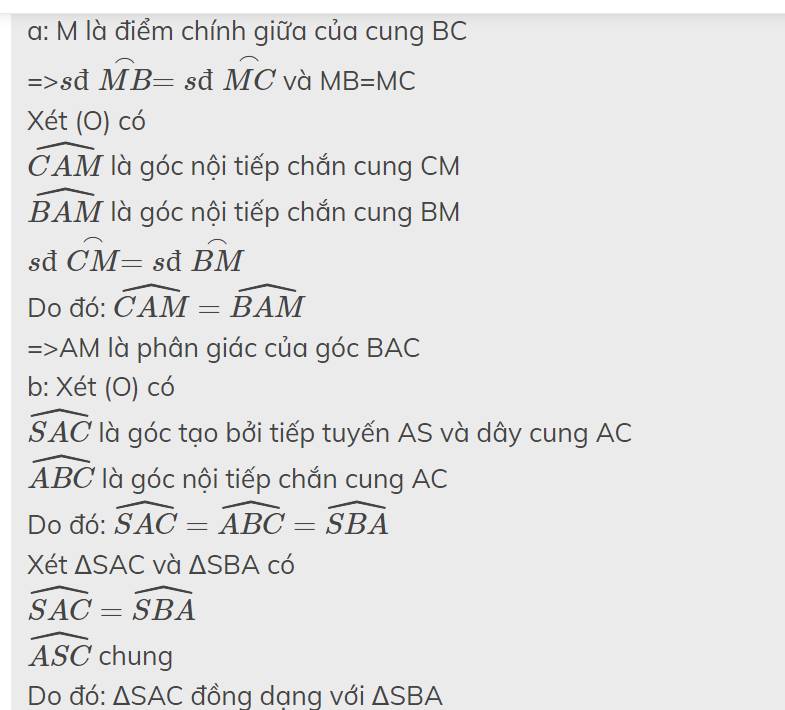
Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R);(AB>AC).Gọi M là điểm chính giữa cung BC; OM cắt BC tại D; AM cắt BC tại K a)chứng minh AM là tia phân giác của BAC b)Tiếp tuyến tại A của đường tròn tâm O cắt BC tại S.Chứng minh SA²=SB.SC c)chứng minh SA=SK và S;A;O;D cùng thuộc 1 đường tròn d)Trên đường tròn tâm O đặt E sao cho SB.SC=SE² chứng minh điểm E nằm trên đường tròn (SAOD)


d: \(SA^2=SB\cdot SC\)
\(SE^2=SB\cdot SC\)
=>SA=SE
Xét ΔOAS và ΔOES có
OA=OE
SA=SE
OS chung
Do đó: ΔOAS=ΔOES
=>\(\widehat{OAS}=\widehat{OES}\)
mà \(\widehat{OAS}=90^0\)
nên \(\widehat{OES}=90^0\)
=>E nằm trên đường tròn đường kính SO
mà S,A,O,D cùng thuộc đường tròn đường kính SO(cmt)
nên E nằm trên đường tròn (SAOD)












