Bài 9: Tính chất ba đường cao của tam giác
Các câu hỏi tương tự
Cho tam giác ABC vuông ở A và có đường cao AH . M , N là trung điểm của BC và AB . Đường thẳng MN cắt tia AH tại D . Kẻ HE vuông góc với AC ; HF vuông góc với AB.
a. Chứng minh : AM vuông góc với EF
b. Chứng minh : EF vuông góc với BD
Cho tam giác ABC, góc A =135 độ,AH là đường cao . Vẽ BK vuông góc AC,CK cắt HA tại E
a, Chứng minh BA vuông góc với EC.
b, Chứng minh AK=BK.
c, So sánh AE và BC.
Cho tam giác ABC vuông tại A kẻ phân giác BD của góc ABC từ d kẻ DE vuông góc với BC tại E a) Chứng minh tam giác BEA cân b) Chứng minh DB là trung trực của AE c) Chứng minh DA
Cho tam giác ABC có AB=AC=5cm BC=6cm đường cao AH xuất phát từ đỉnh A của tam giác ABC (H thuộc BC) a)chứng minh tam giác AHB =AHC b)chứng minh AH là tia phân giác của góc A c)tính độ dài các đoạn thẳng BH và AH
cho tam giác abc vuông tại a kẻ đường cao ah lấy điểm k thuộc doạn thẳng hc qua k kẻ đường thắngong song với ab cắt ah tại d chứng minh ak vuông góc cd
Cho ∆abc vuông tại a có ab=6cm, ac=8cm. Tia phân giác của góc abc cắt ac tại d.
a)Tính bc
b) Kẻ ah vuông góc với bc, tia ah cắt bc tại k. Chứng minh:∆ahb=∆khb
c) Chứng minh:dk vuông góc với bc
d) Qua c kẻ đường thẳng song song với ak, cắt tia ba tại e. Chứng minh:2(ad+ae)>ec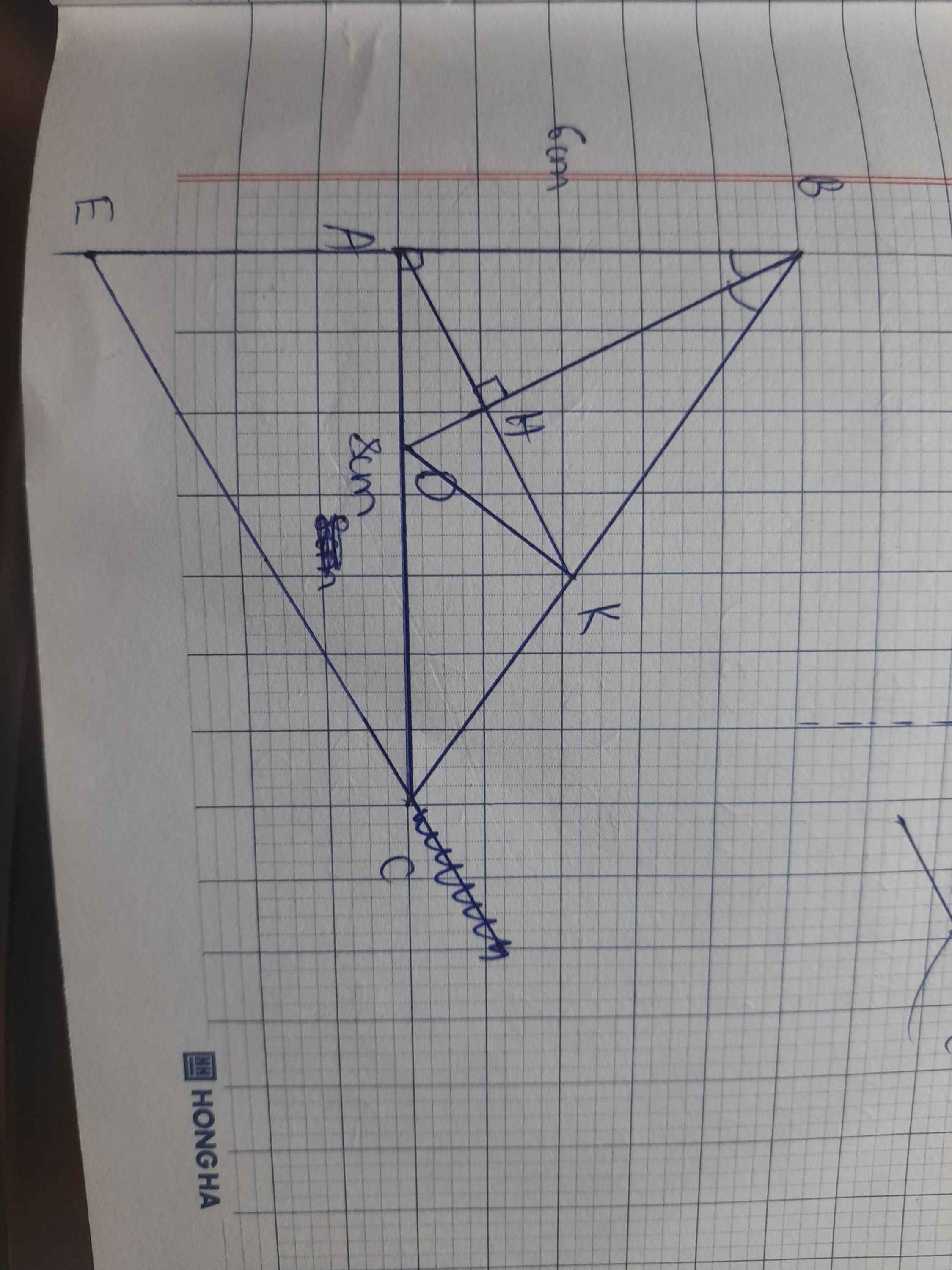
Bài 18. Cho tam giác ABC có AB AC BC và H là trực tâm. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?a) H là giao điểm ba đường trung trực của tam giác ABC.b) CH vuông góc với AB.c) AH vuông góc với BC.
Đọc tiếp
Bài 18. Cho tam giác ABC có AB > AC > BC và H là trực tâm. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) H là giao điểm ba đường trung trực của tam giác ABC.
b) CH vuông góc với AB.
c) AH vuông góc với BC.
Cho ABC vuông tại A có ( AB < AC ) , từ A vẽ AH vuông góc với BC tại H ( HE BC ) , trên tỉa AH lấy điểm D sao cho AH = HD . a ) Cm : AABH = ADBH b ) Cm : AACD cân c ) Lấy điểm E thuộc đoạn thẳng HC sao cho BH = HE , DE cắt AC tại I. Cm : IC < EC
Cho tam giác ABC vuông tại A, AK là đường cao. Gọi M,N lần lượt là hình chiếu của K trên AB, AC. Gọi D là trung điểm AB và I là điểm đối xứng của A qua K. Chứng minh CD vuông góc IN










