\(S_{DEF}=S_{BDF}+S_{DCE}+S_{AFE}+S_{ABC}=2\left(S_{ABD}+S_{BCE}+S_{AFC}\right)+S_{ABC}=2.\left(S_{ABC}+S_{ABC}+S_{ABC}\right)+S_{ABC}=7.S_{ABC}\)
Ôn tập: Tam giác đồng dạng
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A (AB>AC). Kẻ đường cao AH (H thuộc BC). Gọi D là trung điểm của AB. Qua A kẻ đường thẳng vuông góc với CD cắt CD và CB lần lượt tại E và F. Gọi K là hình chiếu vuông góc của D trên BC.
1) Chứng minh rằng các tam giác ADE và CDA đồng dạng với nhau.
2) Chứng minh rằng BD.BC = BE.CD.
Bổ Toán Bổ Đề Về Tính Chất Đường Phân Giác Trong Tam Giác Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của đoạn thẳng BC. Gọi D và E là hai điểm lần lượt thuộc AB và AC sao cho widehat{DME}widehat{ABC}a) Chứng minh rằng tam giác BMD đồng dạng với tam giác CEM.b) Chứng minh rằng DM là tia phân giác của góc widehat{BDE}.P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em tham khảo với ạ!Em cám ơn nhiều ạ!
Đọc tiếp
Bổ Toán Bổ Đề Về Tính Chất Đường Phân Giác Trong Tam Giác
'' Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của đoạn thẳng BC. Gọi D và E là hai điểm lần lượt thuộc AB và AC sao cho \(\widehat{DME}=\widehat{ABC}\)
a) Chứng minh rằng tam giác BMD đồng dạng với tam giác CEM.
b) Chứng minh rằng DM là tia phân giác của góc \(\widehat{BDE}\).
P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều ạ!
Cho tam giác ABC cân tại đỉnh A , có đường cao AH. Gọi M là 1 điểm di động trên cạnh BC. Điểm D và E lần lượt thuộc cạnh AB và AC sao cho tứ giác ADME là hình bình hành. Gọi I là giao điểm của BE và CD.a) Chứng minh rằng : widehat{DMI}widehat{AME}b) Chứng minh rằng đường thẳng MI luôn luôn đi qua 1 điểm cố định .P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ, em cám ơn nhiều lắm ạ!
Đọc tiếp
Cho tam giác ABC cân tại đỉnh A , có đường cao AH. Gọi M là 1 điểm di động trên cạnh BC. Điểm D và E lần lượt thuộc cạnh AB và AC sao cho tứ giác ADME là hình bình hành. Gọi I là giao điểm của BE và CD.
a) Chứng minh rằng : \(\widehat{DMI}=\widehat{AME}\)
b) Chứng minh rằng đường thẳng MI luôn luôn đi qua 1 điểm cố định .
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ, em cám ơn nhiều lắm ạ!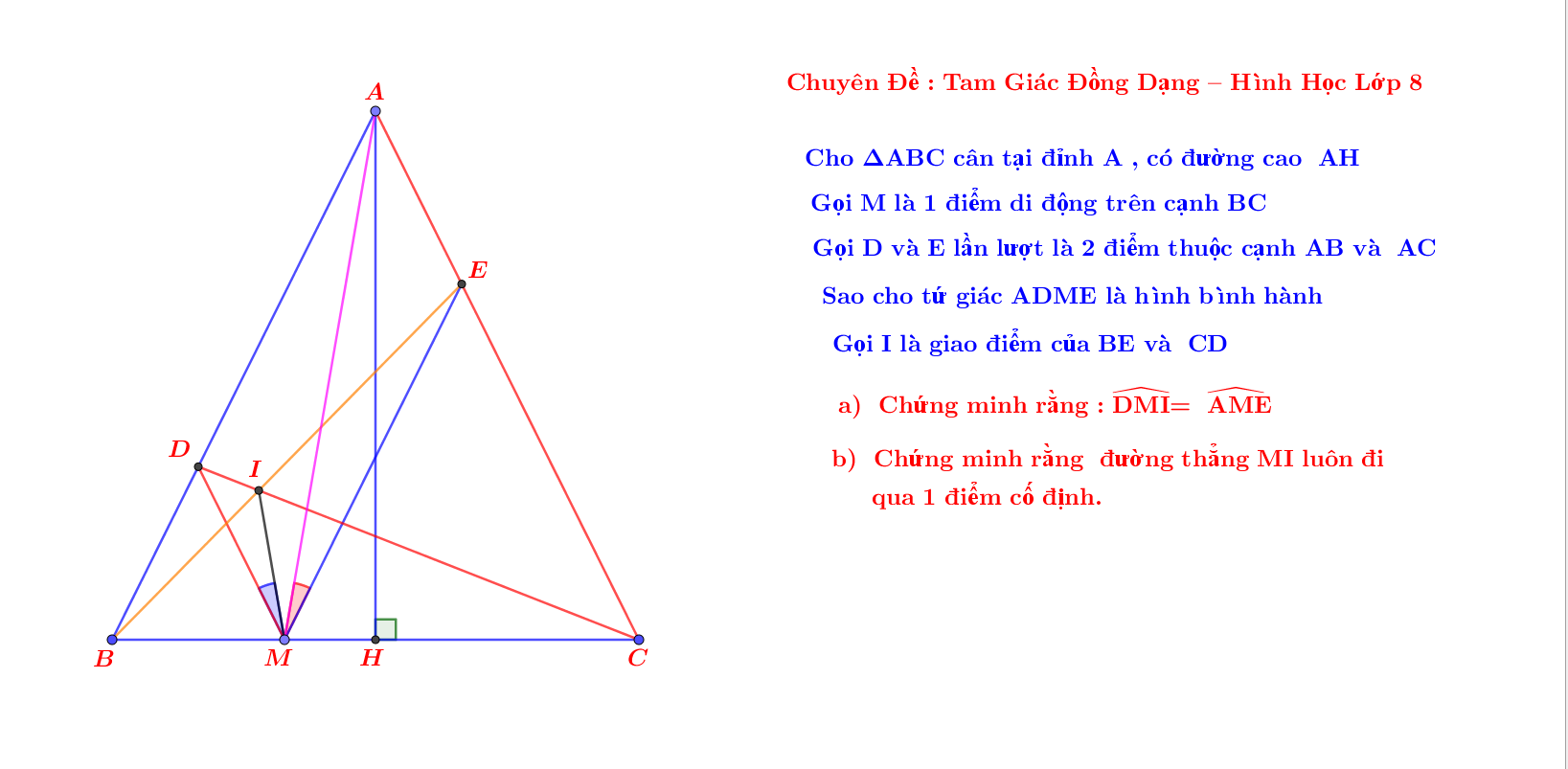
Cho hình bình hành ABCD. Qua A kẻ một đường thẳng bất kì cắt BD, DC, BC lần lượt tại E, F, G.
a. Chứng minh rằng: tam giác DAE đồng dạng tam giác BFE
b. AB . AG = . AF . DG
c. AE^2 = EF . EG
d. Tích BF . DG không đổi
e. Cho AB = 10 cm, AD = 9 cm, DG = 6 cm. Tính độ dài BG và CM và 9 lần dt tam giác BEA = 25 lần dt tam giác DEG
Giúp mình vs *-*
Cho hình vuông ABCD có AB = a, hai đường chéo cắt nhau tại O. Trên hai cạnh AB, BC lần lượt lấy hai điểm E và G sao cho AE= BG. Gọi H là giao điểm của tia AG và tia DC, I là giao điểm của tia OG và đoạn thẳng BH.
1) Chứng minh rằng: AOGE là tam giác vuông cân.
ChoΔABC. Lấy P ở miền ngoài tam giác, thuộc miền trong ∠Acx (Cx là tia đối của tia CB). Từ P kẻ các đường vuông góc với các đường thẳng AC, BC, CD ( D là trung điểm của AB), chúng lần lượt cắt đường cao CH tại X, Y, Z. Chứng minh rằng:
a) ΔPZY ∼ Δ CDB;
b)ΔPXZ ∼ ΔCAD;
c) YZ = ZX.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB và ACa) Chứng minh rằng ΔAEF ΔACBb) Cho AH 4,8cm, BC 10 cm. Tính SAEF?c) Lấy điểm I đối xứng với H qua AB. Từ B kẻ đường vuông góc với BC cắt AI ở K. Chứng minh rằng KC, AH, EF đồng quy
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB và AC
a) Chứng minh rằng ΔAEF ![]() ΔACB
ΔACB
b) Cho AH = 4,8cm, BC = 10 cm. Tính SAEF?
c) Lấy điểm I đối xứng với H qua AB. Từ B kẻ đường vuông góc với BC cắt AI ở K. Chứng minh rằng KC, AH, EF đồng quy
Cho tam giác abc vuông tại A ah là dường cao
a)chứng minh tam giác abc đồng dạng tam giác abh,AB^2=BH.BC
b)gọi d e lần lượt là trung điểm ah,bh.Chứng minh tam giác abe đồng dạng tam giác acd
c) cd giao ae tại k;ed giao ac tại k;kh giao ed tại i.CHỨNG MINH DI.EF=DF.EI
Cho ∆ABC vuông tại A có đường cao AD gọi E,F lần lượt là hình chiếu vuông góc của D lên cạnh AB,AC a) chứng minh tam giác ∆BDA ~ ∆BAC b)Chứng minh AE . AB = AF . AC c) Chứng minh: EF³= BE.CF.BC











