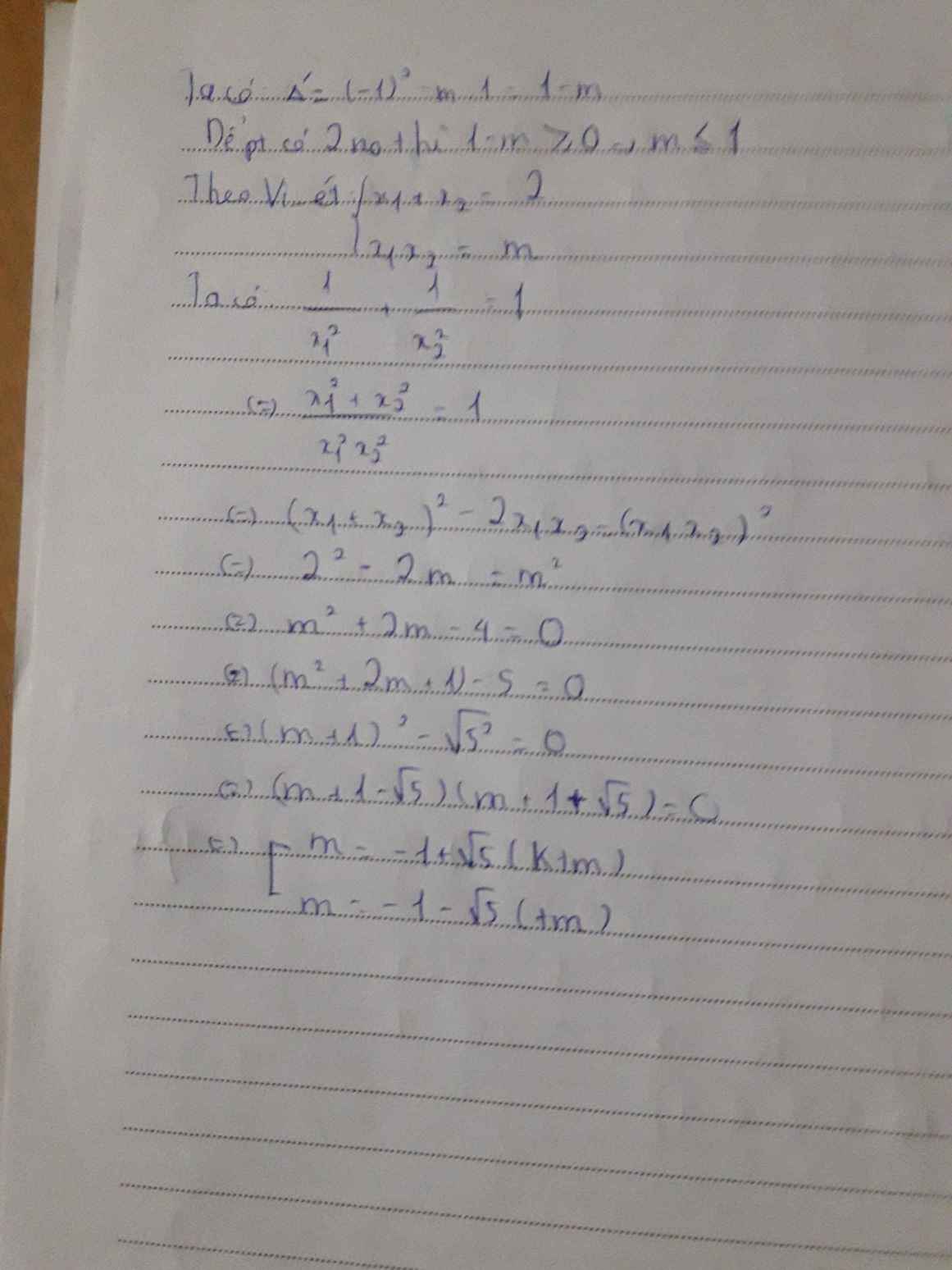Phương trình có nghiệm \(\Leftrightarrow\Delta'\ge0\Leftrightarrow1-m\ge0\Leftrightarrow m\le1\)
Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m\end{matrix}\right.\) (1)
Ta có: \(\dfrac{1}{x^2}+\dfrac{1}{x^2}=1\Leftrightarrow\dfrac{x^2_1+x^2_2}{x^2_1x^2_2}=1\Leftrightarrow\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{\left(x_1x_2\right)^2}=1\) (2)
Từ (1) và (2) \(\Rightarrow4-2m=m^2\Leftrightarrow m^2+2m-4=0\)
\(\Delta'=1+4=5\Rightarrow\sqrt{\Delta'}=\sqrt{5}\Rightarrow\left[{}\begin{matrix}m=-1+\sqrt{5}\left(\text{loại}\right)\\m=-1-\sqrt{5}\left(\text{nhận}\right)\end{matrix}\right.\)
Vậy \(m=-1-\sqrt{5}\)