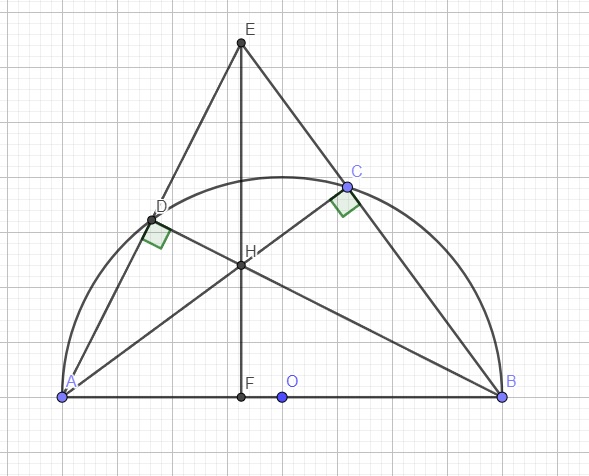
CHo nửa đương tròn tâm O, đường kính AB. Điểm C trên nửa đường tròn ( C khác A và B) gọi D là điểm chính giữa cung AC. Tia AD cắt tia BC tại E, AC cắt BD tại h, tia EH cắt đường kính AB tại F1) CM 4 điểm C,E,D,H cùng thuộc đường tròn. Xác định tâm của đường tròn2) CM HC.HA-HD.HB và tam giác HCF là tam giác cân
a.
AB là đường kính và C, D thuộc đường tròn nên \(\widehat{ACB};\widehat{ADB}\) là các góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=\widehat{ADB}=90^0\)
\(\Rightarrow\widehat{HCE}=\widehat{HDE}=90^0\)
\(\Rightarrow\) C và D cùng nhìn HE dưới 1 góc vuông nên C, E, D, H cùng thuộc đường tròn đường kính HE
Tâm của đường tròn này là trung điểm HE.
b.
Xét hai tam giác HDA và HCB có:
\(\left\{{}\begin{matrix}\widehat{HDA}=\widehat{HCB}=90^0\\\widehat{AHD}=\widehat{BHC}\left(đối-đỉnh\right)\end{matrix}\right.\)
\(\Rightarrow\Delta HDA\sim\Delta HCB\left(g.g\right)\)
\(\Rightarrow\dfrac{HD}{HC}=\dfrac{HA}{HB}\Rightarrow HC.HA=HD.HB\)
Theo câu a, \(\widehat{ACB}=\widehat{ADB}=90^0\Rightarrow\left\{{}\begin{matrix}AC\perp BE\\BD\perp AE\end{matrix}\right.\)
\(\Rightarrow H\) là trực tâm tam giác ABE
\(\Rightarrow EH\) là đường cao thứ 3
\(\Rightarrow EH\) vuông góc AB tại F \(\Rightarrow\Delta BHF\) vuông tại F
D là điểm chính giữa cung AC \(\Rightarrow sđ\stackrel\frown{AD}=sđ\stackrel\frown{CD}\)
\(\Rightarrow\widehat{ABD}=\widehat{CBD}\) (2 góc nt chắn 2 cùng bằng nhau)
Xét hai tam giác vuông BHC và BHF có:
\(\left\{{}\begin{matrix}HB-chung\\\widehat{CBD}=\widehat{ABD}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta_{\perp}BHC=\Delta_{\perp}BHF\left(ch-gn\right)\)
\(\Rightarrow HC=HF\)
\(\Rightarrow\Delta HCF\) cân tại H