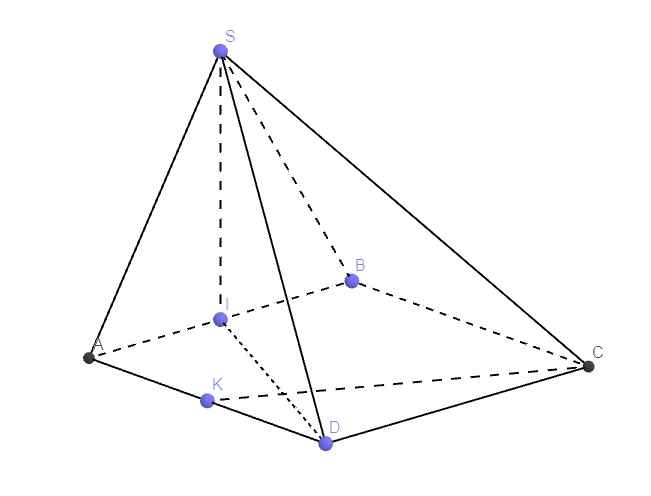
Do tam giác SAB cân và I là trung điểm AB \(\Rightarrow SI\perp AB\)
Mặt khác AB là giao tuyến của hai mặt phẳng vuông góc (SAB) và (ABCD)
\(\Rightarrow SI\perp\left(ABCD\right)\)
\(\Rightarrow SI\perp AD\) (1)
Lại có \(AD\perp AB\) (2) (giả thiết)
(1);(2)\(\Rightarrow AD\perp\left(SAB\right)\)
Mà \(AD\in\left(SAD\right)\Rightarrow\left(SAD\right)\perp\left(SAB\right)\)
b.
Theo cmt ta có \(\left\{{}\begin{matrix}SI\perp\left(ABCD\right)\\SI\in\left(SID\right)\end{matrix}\right.\) \(\Rightarrow\left(SID\right)\perp\left(ABCD\right)\)
c.
\(\overrightarrow{ID}.\overrightarrow{CK}=\left(\overrightarrow{IA}+\overrightarrow{AD}\right)\left(\overrightarrow{CD}+\overrightarrow{DK}\right)=\left(-\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\right)\left(-\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\right)\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}AD^2+\dfrac{1}{4}\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AD}\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}AD^2\) (do AB vuông góc AD nên \(\overrightarrow{AB}.\overrightarrow{AD}=0\))
\(=0\) (ABCD là hình vuông nên AB=AD)
\(\Rightarrow ID\perp CK\)
Mà \(SI\perp\left(ABCD\right)\Rightarrow SI\perp CK\)
\(\Rightarrow CK\perp\left(SID\right)\)
\(\Rightarrow\left(SKC\right)\perp\left(SID\right)\)