Bài 4: Khái niệm hai tam giác đồng dạng
Các câu hỏi tương tự
cho hình bình hành ABCD. Một đường thẳng tam giác đi qua A, cắt BD,BC,DC theo thứ tự tại các điểm E,F,G
a)CM hai △DAE và △BFE đồng dạng, hai △DGE và △BEA đồng dạng
b)CM hệ thức: AE2=EF.EG
c)CM tính BF.DG không phụ thuộc vào vị trí của tam giác khi tam giác quay xung quanh đỉnh A
giúp mk nhanh chút nha
Hình thang ABCD (AB//CD) có CD = 2AB. Gọi E là trung điểm của DC (h.21).
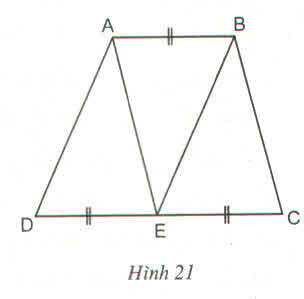
Chứng minh rằng 3 tam giác ADE, ABE và BEC đồng dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau)
cho hình thang abcd (ab//cd) có m là giao điểm của ad và c, n là giao điểm của hai đường chéo .Gọi i và k theo thứ tự là giao điểm cua mn vói ab và cd.Chứng minh rằng :
a)ai/dk=ib/kc,ai/kc=ib/dk
b)i là trung điểm của ab,k là trung điểm của cd
Cho hình thang ABCD (AB//CD). Gọi O là giao điểm của hai đường chéo AC và BD. Qua O kẻ đường thẳng d song song với AB, d cắt AD và BC theo thứ tự ở M và N
a)Chứng minh AM/AD=BN/BC
b)Chứng minh OM=ONv
Cho tam giác nhọn ABC có góc C = 40 độ. Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của các tam giác ABC, ACD
a) Chứng minh rằng tam giác AKH đồng dạng với tam giác BCA
b) Tính số đo góc AKH
Cho hình thang ABCD có AB = AD = 1/2 CD. Gọi M là trung điểm của CD. Gọi H là gia điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh DB vuông góc BC
c) CM: tam giác ADH đồng dạng với tamn giác CDB
d) Biết AB=2,5cm;BD=4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD
giúp mk vs
cho tam giác ABC nhọn, AB<AC .Trên cạnh AB lấy điểm D(D khác A và B),trên cạnh AC lấy điểm E sao cho góc ADE = ACB
a) CM : tam giác ADE đồng dạng tam giác ACB
b)Gọi i là giao điểm của BC và DE. CM: IB.IC=ID.IE
c)Lấy M là trung điểm BC . CM \(\dfrac{AD.AB}{AE.AM}\) =2
cho tam giác ABC vuông tại A có ABAC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC. a/ chứng minh: tam giác ABC đồng dạng với tam giác HBA từ đó suy ra AB^2 BC.CHb/ Chứng minh: AE.ABAF.ACC/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCAMỌI NGƯỜI GIÚP MÌNH VỚI Ạ!!!
Đọc tiếp
cho tam giác ABC vuông tại A có AB<AC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC.
a/ chứng minh: tam giác ABC đồng dạng với tam giác HBA từ đó suy ra AB^2= BC.CH
b/ Chứng minh: AE.AB=AF.AC
C/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCA
MỌI NGƯỜI GIÚP MÌNH VỚI Ạ!!!
cho tam giác ABC vuông tại A có ABAC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC. a/ chứng minh: tam giác ABC đồng dạng với tam giác HCA từ đó suy ra AB^2 BC.CHb/ Chứng minh: AE.ABAF.ACC/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCAMỌI NGƯỜI GIÚP MÌNH VỚI Ạ
Đọc tiếp
cho tam giác ABC vuông tại A có AB<AC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC.
a/ chứng minh: tam giác ABC đồng dạng với tam giác HCA từ đó suy ra AB^2= BC.CH
b/ Chứng minh: AE.AB=AF.AC
C/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCA
MỌI NGƯỜI GIÚP MÌNH VỚI Ạ









