Lời giải
a)
Kẻ đường thẳng d qua M // với hai đáy
cắt AD tại P cắt BC tại Q cắt AC tại N'
Ta c/m N trùng N'
xét \(\Delta_{DBC}\) có MQ là đường trung bình tam giác => BQ=QC
PQ//DC => PQ là đường TB của Hình Thang ABCD => P là trung điểm của AD
xét \(\Delta_{DAC}\) có PQ là đường trung bình =>AN'=N'C
=> N' trùng N => MN //AB//CD=> dpcm
b)
???
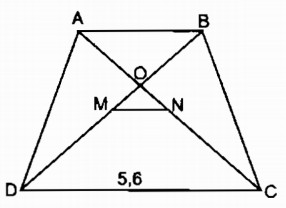
a) Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ∆ADC và ∆BCD, ta có:
AC = BD (chứng minh trên )
AD = BC (ABCD cân)
CD cạnh chung
\(\Rightarrow\Delta ACD=\Delta BCD\left(c.c.c\right)\)
\(\Rightarrow\widehat{ACD}=\widehat{BDC}\)
Hay \(\widehat{OCD}=\widehat{ODC}\)
Suy ra tam giác OCD cân tại O
Suy ra: (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Lại có: \(MD=3MO\left(gt\right)\Rightarrow NC=3NO\)
Trong tam giác OCD, ta có: \(\dfrac{MO}{MD}=\dfrac{NO}{NC}=\dfrac{1}{3}\)
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét )
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong tam giác OCD, ta có: MN // CD
\(\Rightarrow\dfrac{OM}{OB}=\dfrac{MN}{AB}\) (Hệ quả định lí Ta-lét)
\(\Rightarrow\dfrac{MN}{AB}=\dfrac{OM}{2OM}=\dfrac{1}{2}\)
Vậy: \(AB=2MN=2.1,4=2,8\left(cm\right)\)
b) Ta có: \(\dfrac{CD-AB}{2}=\dfrac{5,6-2,8}{2}=\dfrac{2,8}{2}=1,4\left(cm\right)\)
Vậy: \(MN=\dfrac{CD-AB}{2}\)














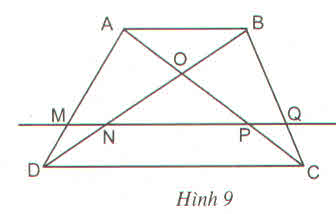 DN\BD=CP\AC
DN\BD=CP\AC


