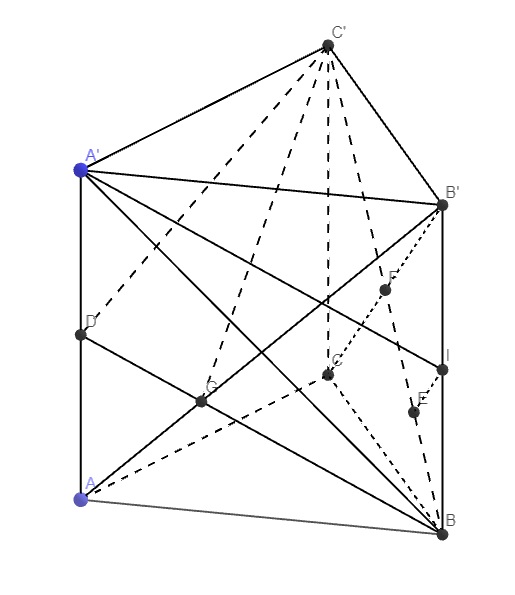
a. Tam giác AA'B vuông cân tại A nên \(\widehat{A'BA}=45^0\)
b.
Gọi D là trung điểm AA'\(\Rightarrow D,B,G\) thẳng hàng
Tứ giác A'IBD là hình bình hành
\(\Rightarrow A'I||BD\Rightarrow A'I||\left(C'BD\right)\Rightarrow d\left(A'I;C'G\right)=d\left(A'I;\left(C'BD\right)\right)=d\left(I;\left(C'BD\right)\right)\)
Gọi F là giao điểm B'C và BC'
Ta có \(DC'=DB=\dfrac{a\sqrt{5}}{2}\) (pitago) \(\Rightarrow\Delta BDC'\) cân tại B
\(\Rightarrow DF\perp BC'\)
Tương tự, \(\Delta CDB'\) cân tại D \(\Rightarrow DF\perp B'C\)
\(\Rightarrow DF\perp\left(BCC'B'\right)\Rightarrow\left(C'BD\right)\perp\left(BCC'B'\right)\)
Từ I kẻ \(IE\perp BC'\Rightarrow IE\perp\left(C'BD\right)\Rightarrow IE=d\left(I;\left(C'BD\right)\right)\)
\(IE=\dfrac{1}{2}B'F=\dfrac{a\sqrt{2}}{4}\) (đường trung bình)
\(\Rightarrow d\left(C'G;A'I\right)=\dfrac{a\sqrt{2}}{4}\)