Question

Cho hình lăng trụ ABC.A'B'C'. Gọi M là trung điểm của BC; N là điểm trên cạnh CC' sao cho CN = 2 NC'

1) Tìm giao điểm I của AB với (A'MN). Tính IA/IB 

2) tìm giao tuyến của (AMC') và (A'NB) 

3) Tìm giao tuyến của (ANB) và (MA'C') 

Answer 1

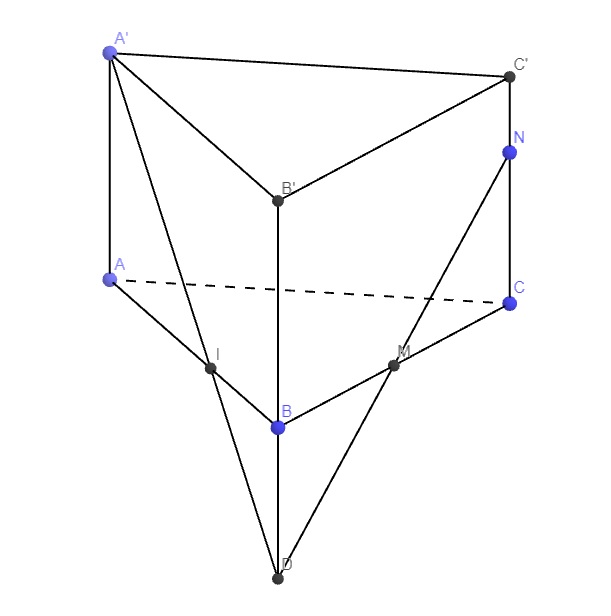
.a

Trong mp (BCC'B') nối MN kéo dài cắt BB' tại D

\(\Rightarrow D\in\left(A'MN\right)\)

Trong mp (ABB'A') nối A'D cắt AB tại I

\(\Rightarrow I=AB\cap\left(A'MN\right)\) 

Do CN song song BD, áp dụng Talet:

\(\dfrac{CN}{BD}=\dfrac{CM}{BM}=1\Rightarrow CN=BD\)

\(\Rightarrow\dfrac{BD}{BB'}=\dfrac{CN}{CC'}=\dfrac{2}{3}\)

Do AA' song song BD, áp dụng Talet:

\(\dfrac{IA}{IB}=\dfrac{AA'}{BD}=\dfrac{BB'}{BD}=\dfrac{3}{2}\)

Các câu này quá nhiều đường nét nên mỗi câu 1 hình riêng cho dễ nhìn:

Answer 2

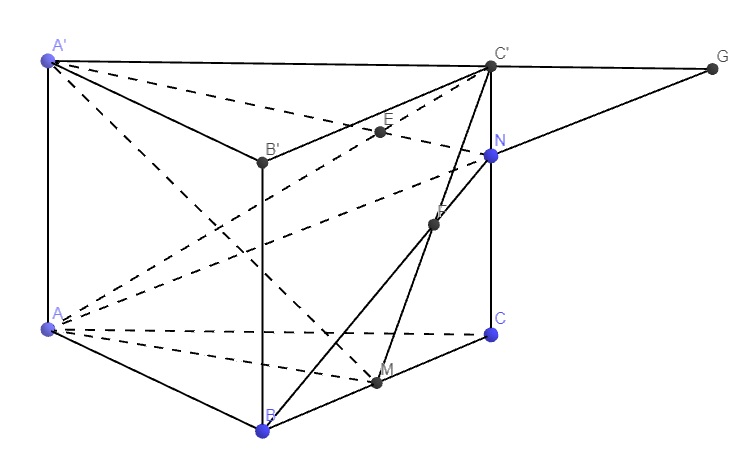
b.

Trong mp (ACC'A'), gọi E là giao điểm A'N và AC'

Trong mp ((BCC'B'), gọi F là giao điểm BN và C'M

\(\Rightarrow EF=\left(AMC'\right)\cap\left(A'NB\right)\)

c.

Trong mp (ACC'A'), kéo dài AN và A'C' cắt nhau tại G

\(\Rightarrow G\in\left(ANB\right)\cap\left(MA'C'\right)\)

\(F=BN\cap C'M\Rightarrow F\in\left(ANB\right)\cap\left(MA'C'\right)\)

\(\Rightarrow FG=\left(ANB\right)\cap\left(MA'C'\right)\)