Question

Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(I\) là trung điểm của \(SD\). Hai mặt phẳng \(\left( {IAC} \right)\) và \(\left( {SBC} \right)\) cắt nhau theo giao tuyến \(Cx\). Chứng minh rằng \(Cx\parallel SB\).

Answer 1

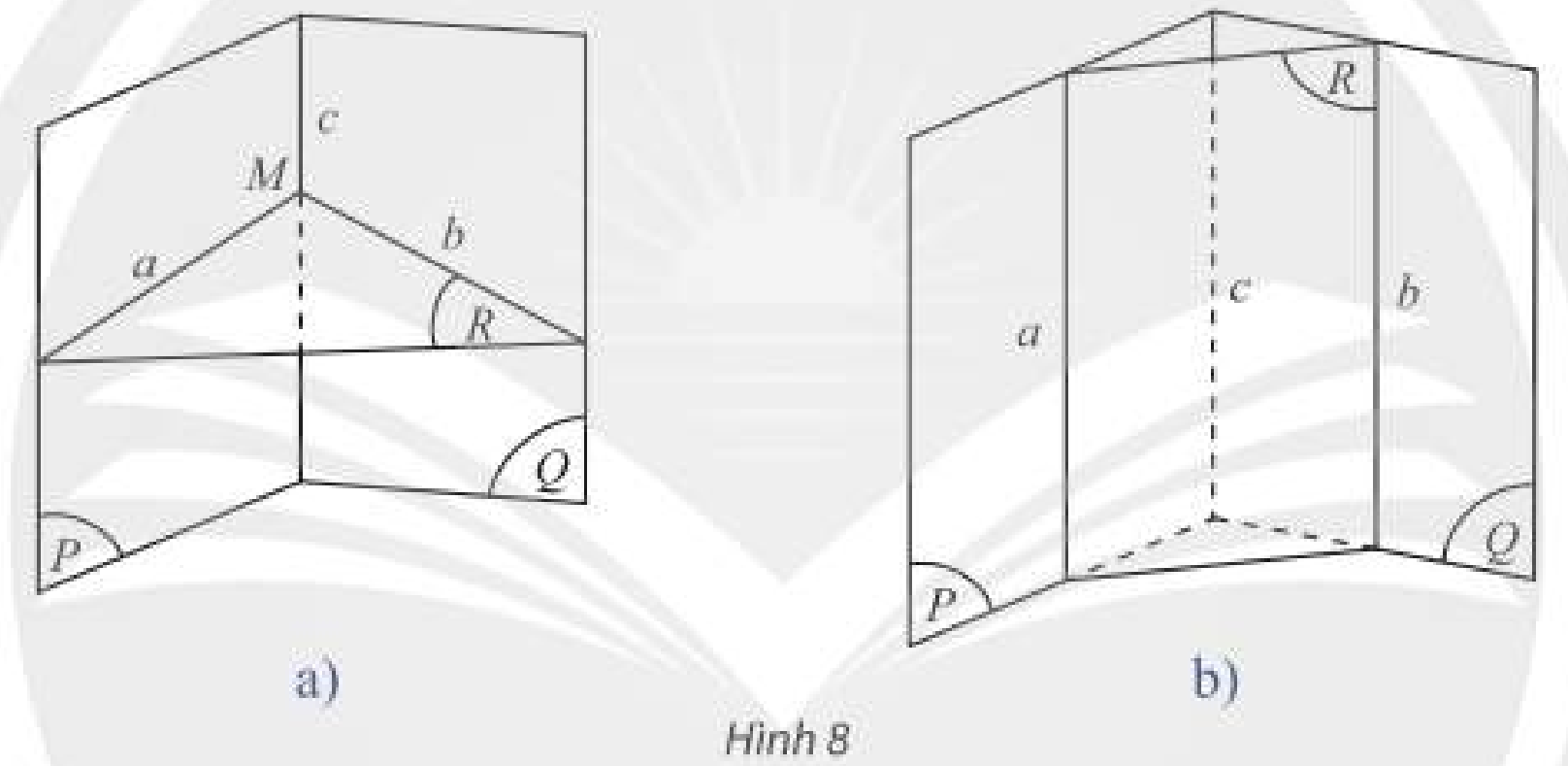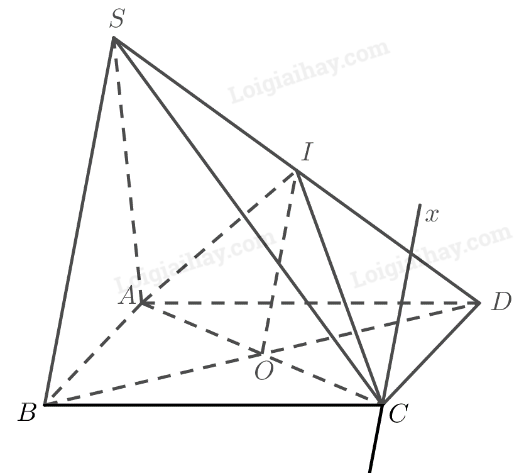
Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Ta có:

\(I\) là trung điểm của \(SD\)

\(O\) là trung điểm của \(BD\) (theo tính chất hình bình hành)

\( \Rightarrow OI\) là đường trung bình của tam giác \(SB{\rm{D}}\)

\( \Rightarrow OI\parallel SB\)

Ta có:

\(\begin{array}{l}Cx = \left( {IAC} \right) \cap \left( {SBC} \right)\\SB = \left( {SB{\rm{D}}} \right) \cap \left( {SBC} \right)\\OI = \left( {IAC} \right) \cap \left( {SB{\rm{D}}} \right)\\SB\parallel OI\end{array}\)

Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(OI\parallel SB\parallel Cx\).