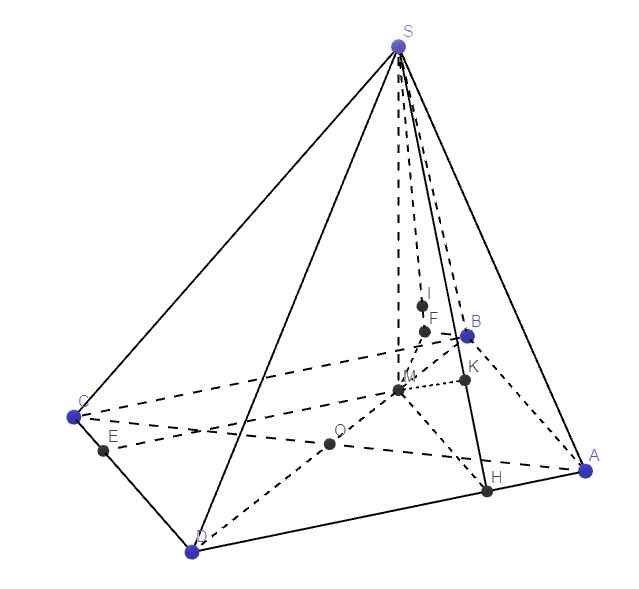
Chắc đề là \(SM=a\sqrt{3}\) vì không có điểm H nào trong dữ liệu
\(BC=AD=\sqrt{BD^2-AB^2}=a\sqrt{2}\)
a.
Qua M kẻ đường thẳng song song BC cắt CD tại E
\(\Rightarrow CD\perp ME\Rightarrow CD\perp\left(SME\right)\)
\(\Rightarrow\widehat{SEM}\) là góc giữa (SCD) và (ABCD)
Áp dụng định lý talet trong tam giác BCD:
\(\dfrac{EM}{BC}=\dfrac{DM}{BD}=\dfrac{3}{4}\Rightarrow EM=\dfrac{3}{4}BC=\dfrac{3a\sqrt{2}}{4}\)
\(\Rightarrow tan\widehat{SEM}=\dfrac{SM}{EM}=\dfrac{2\sqrt{6}}{3}\)
\(\Rightarrow\widehat{SEM}\approx58^031'\)
b.
\(BC||AD\Rightarrow BC||\left(SAD\right)\)
\(\Rightarrow d\left(BC;AD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Lại có: BM cắt (SAD) tại D, mà \(BD=\dfrac{4}{3}MD\)
\(\Rightarrow d\left(B;\left(SAD\right)\right)=\dfrac{4}{3}d\left(M;\left(SAD\right)\right)\)
Trong mp (ABCD), từ M kẻ \(MH\perp AD\)
Trong mp (SMH), từ M kẻ \(MK\perp SH\)
\(\Rightarrow MK\perp\left(SAD\right)\Rightarrow MK=d\left(M;\left(SAD\right)\right)\)
Talet cho tam giác ABD:
\(\dfrac{MH}{AB}=\dfrac{MD}{BD}=\dfrac{3}{4}\Rightarrow MH=\dfrac{3}{4}AB=\dfrac{3a}{4}\)
Hệ thức lượng trong tam giác vuông SMH:
\(MK=\dfrac{SM.MH}{\sqrt{SM^2+MH^2}}=\dfrac{3a\sqrt{19}}{19}\)
\(\Rightarrow d\left(SD;BC\right)=\dfrac{4}{3}MK=\dfrac{4\sqrt{19}}{19}\)
c.
Qua B kẻ đường thẳng d song song AC
Trong mp (ABCD), từ M hạ \(MF\perp d\)
\(AC||d\Rightarrow AC||\left(SBF\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SBF\right)\right)=d\left(O;\left(SBF\right)\right)\)
Mà \(OM\) cắt \(\left(SBF\right)\) tại B đồng thời \(OB=2MB\)
\(\Rightarrow d\left(O;\left(SBF\right)\right)=2d\left(M;\left(SBF\right)\right)\)
Trong mp (SMF), từ M hạ \(MI\perp SF\)
\(\Rightarrow MI\perp\left(SBF\right)\Rightarrow MI=d\left(M;\left(SBF\right)\right)\)
Ta có: \(\widehat{MBF}=\widehat{AOB}\) (so le trong)
\(cos\widehat{AOB}=\dfrac{OA^2+OB^2-AB^2}{2OA.OB}=\dfrac{1}{3}\)
\(\Rightarrow cos\widehat{MBF}=\dfrac{1}{3}\Rightarrow MF=BM.cos\widehat{MBF}=\dfrac{1}{4}BD.\dfrac{1}{3}=\dfrac{a\sqrt{3}}{12}\)
Áp dụng hệ thức lượng trong tam giác vuông SMF:
\(MI=\dfrac{SM.MF}{\sqrt{SM^2+MF^2}}=...\)
\(\Rightarrow d\left(SB;AC\right)=2MI=...\)