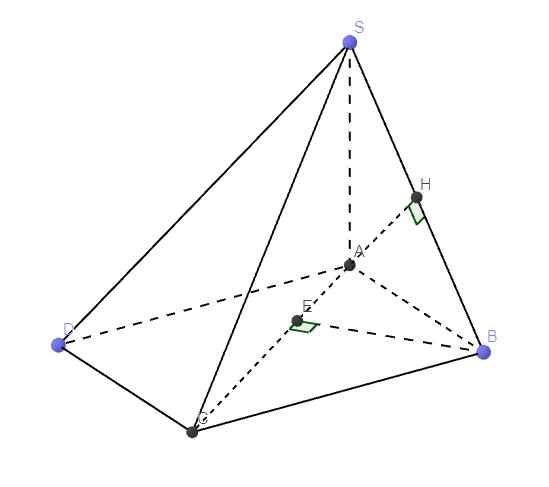
Ta có:
\(\left\{{}\begin{matrix}BH\cap\left(SAC\right)=S\\BS=2HS\end{matrix}\right.\) \(\Rightarrow d\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(B;\left(SAC\right)\right)\)
Từ B kẻ \(BE\perp AC\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BE\\BE\perp AC\end{matrix}\right.\) \(\Rightarrow BE\perp\left(SAC\right)\)
\(\Rightarrow BE=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BE^2}=\dfrac{1}{AB^2}+\dfrac{1}{BC^2}=\dfrac{3}{2a^2}\Rightarrow BE=\dfrac{a\sqrt{6}}{3}\)
\(\Rightarrow h\left(H;\left(SAC\right)\right)=\dfrac{1}{2}BE=\dfrac{a\sqrt{6}}{6}\)
b.
Ta có: \(CD||AB\Rightarrow CD||\left(SAB\right)\)
Mà \(AH\in\left(SAB\right)\Rightarrow d\left(AH,CD\right)=d\left(CD;\left(SAB\right)\right)=d\left(D;\left(SAB\right)\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\Rightarrow AD=d\left(D;\left(SAB\right)\right)\)
\(\Rightarrow d\left(AH;CD\right)=AD=a\sqrt{2}\)