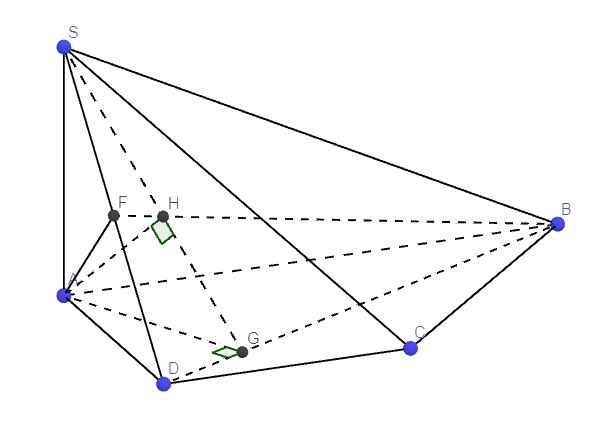
Kẻ \(AF\perp SD\) ; \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AF\)
\(\Rightarrow AF\perp\left(SCD\right)\)
Kẻ \(AG\perp BD\) ; trong mp (SBD) kẻ \(AH\perp SG\)
\(\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow\widehat{FAH}\) là góc giữa (SCD) và (SBD)
\(AH\perp\left(SBD\right)\Rightarrow AH\perp FH\Rightarrow\Delta FAH\) vuông tại H
Tam giác SAD vuông cân tại A \(\Rightarrow AF=\dfrac{1}{2}SD=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng tam giác SBD: \(\dfrac{1}{AG^2}=\dfrac{1}{AD^2}+\dfrac{1}{AB^2}=\dfrac{5}{4a^2}\)
Hệ thức lượng tam giác SAG: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AG^2}=\dfrac{1}{a^2}+\dfrac{5}{4a^2}=\dfrac{9}{4a^2}\Rightarrow AH=\dfrac{2a}{3}\)
\(\Rightarrow cos\widehat{FAH}=\dfrac{AH}{AF}=\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\widehat{FAH}\approx19^028'\)