Chương 2: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG
Các câu hỏi tương tự
Cho hình bình hành ABCD. Gọi N là trung điểm cạnh CD. Trên cạnh AC lấy điểm M sao cho AM = 2MC; Phân tích các vec tơ sau theo hai véc tơ ABvà AD
a. vecto ac
b) vecto AM
c) vecto an
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức (1.0 điểm). Chứng minh đẳng thức .
Đọc tiếp
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức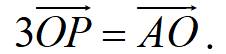
(1.0 điểm). Chứng minh đẳng thức .
cho hình vuông ABCD có cạnh bằng 3. I là trung điểm AB. Tích vecto BI.CA
Cho hình thang ABCD có \(\overrightarrow{2AB}=\overrightarrow{DC}\),AC=8,BD=6,góc tạo bởi 2 vecto \(\overrightarrow{AC}\) và \(\overrightarrow{BD}\) bằng 120.Tính độ dài các cạnh AD,BC
cho hbh abcd gọi m n lần lượt là hai điểm nằm trên hai cạnh ab và cd sao cho ab =3AM CD=2CN Biểu diễn vectơ AN qua các vectơ AB và AC
Cho hình chữ nhật ABCD
a)Lấy M trên cạnh AD sao cho AM=3DM,N là trung điểm BM.CN theo AB,AD
b)Dựng điểm K sao cho 2Ak-DK+CK=2AB
1.cho bốn điểm A(1.1), B(2,-1), C(4,3) và D(16,3). Hãy biểu diễn vecto AD theo vecto AB,AC
2. cho A(3,4), B(2,5). Tìm X để C(-7,X) thuộc đường thẳng AB
3.cho bốn điểm A(0,1), B(1,3), C(2,7), D(0,3). chứng minh đường thẳng AB//CD
4. cho tâm giác ABC có A(1,-1),B(5,-3) đỉnh C trên Oy và trọng tâm G trên Ox. Tìm tọa độ đỉnh C
5. cho A(-2,1), B(4,5). tìm tọa độ trung điểm I của đoạn AB và tọa độ điểm C sao cho tứ giác OABC là hình bình hành, O là gốc tọa độ
Đọc tiếp
1.cho bốn điểm A(1.1), B(2,-1), C(4,3) và D(16,3). Hãy biểu diễn vecto AD theo vecto AB,AC
2. cho A(3,4), B(2,5). Tìm X để C(-7,X) thuộc đường thẳng AB
3.cho bốn điểm A(0,1), B(1,3), C(2,7), D(0,3). chứng minh đường thẳng AB//CD
4. cho tâm giác ABC có A(1,-1),B(5,-3) đỉnh C trên Oy và trọng tâm G trên Ox. Tìm tọa độ đỉnh C
5. cho A(-2,1), B(4,5). tìm tọa độ trung điểm I của đoạn AB và tọa độ điểm C sao cho tứ giác OABC là hình bình hành, O là gốc tọa độ
Trong mặt phẳng toạ độ Oxy cho tam giác ABC có : A(3,1) B(5,3) C(-1,1)
a) chứng tỏ tam giác ABC vuông cân
b) Tìm toạ độ của điểm M biết vecto MA - 2 vecto MB + 4 vecto MC = vector 0
c) tính diện tích tam giác ABC
d) Tìm N thuộc Oy để NB + NC nhỏ nhất
Câu 38. Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn 3|MA+MB| 2 |MA+ MB + MC| Câu 37. Trong mặt phẳng Oxy, cho tam giác ABC, có A(1;5), B(-2;2), C(3; - 1) . a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b. Tìm tọa độ điểm E sao cho A là trung điểm đoạn BE. c. Tìm tọa độ điểm F sao cho B là trọng tâm tam giác ACF.
Đọc tiếp
Câu 38. Cho tam giác ABC. Tìm tập hợp điểm M thỏa mãn 3|MA+MB| =2 |MA+ MB + MC| Câu 37. Trong mặt phẳng Oxy, cho tam giác ABC, có A(1;5), B(-2;2), C(3; - 1) . a. Tìm tọa độ điểm D sao cho ABCD là hình bình hành. b. Tìm tọa độ điểm E sao cho A là trung điểm đoạn BE. c. Tìm tọa độ điểm F sao cho B là trọng tâm tam giác ACF.










