vecto AN=vecto AC+vecto CN
=vecto AC+1/2vecto CD
=vecto AC+1/2vecto BA
=vecto AC-1/2vecto AB
vecto AN=vecto AC+vecto CN
=vecto AC+1/2vecto CD
=vecto AC+1/2vecto BA
=vecto AC-1/2vecto AB
Cho hình bình hành ABCD. Gọi N là trung điểm cạnh CD. Trên cạnh AC lấy điểm M sao cho AM = 2MC; Phân tích các vec tơ sau theo hai véc tơ ABvà AD
a. vecto ac
b) vecto AM
c) vecto an
Cho hình bình hành ABCD,có tâm O:
a) Tìm điểm I thỏa đẳng thức vecto: IA+IB+IC=BC
b) Gọi M nằm trên cạnh DC sao cho 2DM=MC.Biểu diễn OM theo 2 vecto AB và AD
cho tứ giác ABCD . Gọi M , N lần luợt là trung điểm của AC và BD . Chứng minh rằng : AB2 + BC2 + CD2 +DA2 = AC2 + BD2 + 4MN2
giúp mình bài này với
cho tứ giác ABCD, gọi M,N,P,Q lần lượt là trung điểm của AB,CD,BC,DA thỏa mãn điều kiện MN+PQ=1/2(AB+BC+CD+DA) thì ABCD là hình bình hành
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD; N là trung điểm của cạnh CD; P là điểm thỏa mãn hệ thức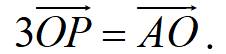
(1.0 điểm). Chứng minh đẳng thức .
Cho tam giác ABC đều cạnh a. M và N là các điểm sao cho 3\(\overrightarrow{BM}\)= 2\(\overrightarrow{BC}\), 5\(\overrightarrow{AN}\) = 4\(\overrightarrow{AC}\)
a, tính \(\overrightarrow{AB}\).\(\overrightarrow{AC}\); \(\overrightarrow{BC}\).\(\overrightarrow{AC}\)
b, cm AM vuông góc BN
cho hình vuông ABCD cạnh a . G ọi N là trung điểm của CD , M là điểm trên AC sao cho AM = \(\frac{1}{4}\) AC : a) tính các cạnh của tam giác BMN ; b) có nhận xét gì về tam giác BMN ? tính diện tích tam giác đó ; c) gọi I là giao điểm của BN và AC , tính CI ; d) tính bán kính đường tròn ngoại tiếp tam giác BDN
Cho hình chữ nhật ABCD
a)Lấy M trên cạnh AD sao cho AM=3DM,N là trung điểm BM.CN theo AB,AD
b)Dựng điểm K sao cho 2Ak-DK+CK=2AB