Ví dụ 1: \(y = 2{x^2} - x - 1\)
Ví dụ 2: \(y = - 3{x^2} + 1\)
Ví dụ 1: \(y = 2{x^2} - x - 1\)
Ví dụ 2: \(y = - 3{x^2} + 1\)
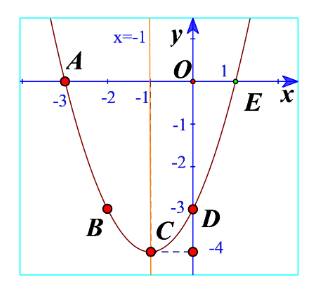
a) Quan sát đồ thị hàm số bậc hai \(y = {x^2} + 2x - 3\) trong Hình 11. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
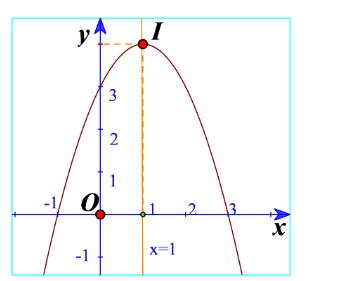
b) Quan sát đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) trong Hình 12. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
Trong các hàm số sau, hàm số nào là hàm số bậc hai? Với những hàm số bậc hai đó, xác định \(a,b,c\) lần lượt là hệ số của \({x^2}\), hệ số của \(x\) và hệ số tự do.
a) \(y = - 3{x^2}\)
b) \(y = 2x\left( {{x^2} - 6x + 1} \right)\)
c) \(y = 4x\left( {2x - 5} \right)\)
Cho đồ thị hàm số bậc hai ở Hình 15.
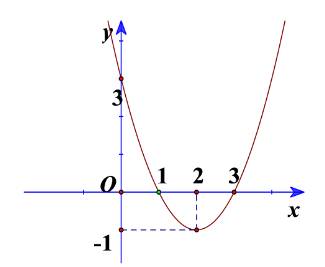
a) Xác định trục đối xứng, tọa độ đỉnh của đồ thị hàm số.
b) Xác định khoảng đồng biến, khoảng nghịch biến của hàm số.
c) Tìm công thức xác định hàm số.
Vẽ đồ thị mỗi hàm số bậc hai sau:
a) \(y = {x^2} - 4x - 3\)
b) \(y = {x^2} + 2x + 1\)
c) \(y = - {x^2} - 2\)
Cho hàm số \(y = - 0,00188{\left( {x - 251,5} \right)^2} + 118\).
a) Viết công thức xác định hàm số trên về dạng đa thức theo lũy thừa với số mũ giảm dần của x.
b) Bậc của đa thức trên bằng bao nhiêu?
c) Xác định hệ số của \({x^2}\), hệ số của x và hệ số tự do.
Cho hàm số \(y = - {x^2} + 2x + 3\).
a) Tìm tọa độ 5 điểm thuộc đồ thị hàm số trên có hoành độ lần lượt là \( - 1,0,1,2,3\) rồi vẽ chúng trong mặt phẳng tọa độ Oxy.
b) Vẽ đường cong đi qua 5 điểm trên. Đường cong đó cũng là đường parabol và là đồ thị của hàm số \(y = - {x^2} + 2x + 3\) (Hình 12).
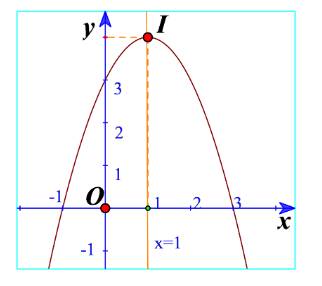
c) Cho biết tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Cho hàm số \(y = {x^2} + 2x - 3\).
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b) Vẽ các điểm \(A\left( { - 3;0} \right),B\left( { - 2; - 3} \right),C\left( { - 1; - 4} \right),\)\(D\left( {0; - 3} \right),E\left( {1;0} \right)\) của đồ thị hàm số \(y = {x^2} + 2x - 3\) trong mặt phẳng tọa độ Oxy.
c) Vẽ đường cong đi qua 5 điểm A, B, C, D, E. Đường cong đó là đường parabol và cũng chính là đồ thị hàm số \(y = {x^2} + 2x - 3\) (Hình 11).
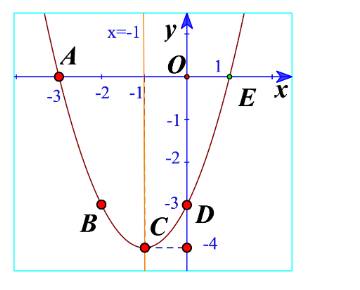
d) Cho biết tọa độ của điểm thấp nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Lập bảng biến thiên của mỗi hàm số sau:
a) \(y = {x^2} - 3x + 4\)
b) \(y = - 2{x^2} + 5\)
Vẽ đồ thị của mỗi hàm số sau:
a) \(y = 2{x^2} - 6x + 4\)
b) \(y = - 3{x^2} - 6x - 3\)