Question

Cho hai tam giác ABC và A'B'C' có kích thước như trong hình 35

a) \(\Delta ABC\) và \(\Delta A'B'C'\) có đồng dạng với nhau không  ? Vì sao ?

b) Tính tỉ số chu vi của hai tam giác đó ?

Answer 1

$\frac{AB}{A^{\prime }{B}^{\prime }}$ = $\frac{BC}{B^{\prime }{C}^{\prime }}$= $\frac{CA}{C^{\prime }{A}^{\prime }}$= 3/2

=> ∆ABC ∽ ∆A'B'C'

b) $\frac{C_{ABC}}{C_{A^{\prime }{B}^{\prime }{C}^{\prime }}}$= 3/2

Answer 2

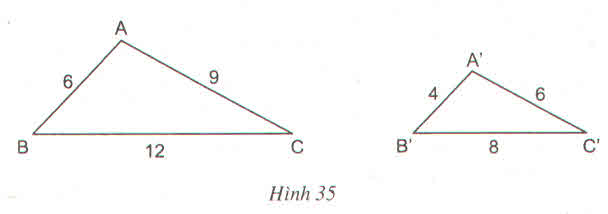
a)Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:

\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}\)

\(\Rightarrow\Delta ABC\)∽\(\Delta A'B'C'\)(c.c.c)

b)Từ câu a và áp dụng tính chất tỉ lệ thức ta có:

\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}=\dfrac{AB+BC+AC}{A'B'+B'C'+A'C'}=\dfrac{3}{2}\)

mà \(C_{ABC}=AB+BC+AC\)

\(C_{A'B'C'}=A'B'+B'C'+A'C'\)

Vậy tỉ số chu vi của \(\Delta ABC\) và \(\Delta A'B'C'\)là:

\(\dfrac{C_{ABC}}{C_{A'B'C'}}=\dfrac{3}{2}\)

Answer 3

a)\(\Delta\)ABC và \(\Delta\)A'B'C' có đồng dạng với nhau

vì:AB/A'B' = BC/B'C' = CA/C'A' = 3/2

b)AB/A'B' = BC/B'C' = CA/C'A' = 3/2

⇔AB+BC+CA/A'B' + B'C' + C'A'

⇔6+12+9/4+8+6 = 3/2