b)
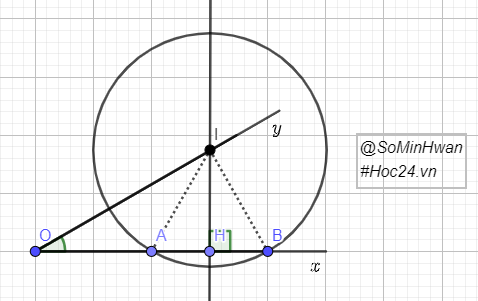
do OA = 2cm , OB = 4cm nên AB = 2cm
Gọi H là giao điểm của đường trung trực AB với đoạn AB thì HA = HB = 1cm,
suy ra : OH = OA + AH = 3cm
tg OHI vuông ở H có góc O = 30o nên OI = 2IH
Theo đl pytago ta có:
\(OI^2=OH^2+HI^2\)
hay \(\left(2IH\right)^2=OH^2+HI^2\);
suy ra 3IH2 = OH2 do đó 3IH2 = 9 suy ra IH2 = 3
tg IAH vuông ở H , nên:
\(IA^2=AH^2+IH^2=1+3=4,=>IA=2\left(cm\right)\)
`b)` Do `OA=2cm,OB=4cm`
`=>AB=2cm`
Gọi `H` là giao điểm đường trung trực `AB` , với đoạn `AB` thì
`HA=HB=1cm`
Suy ra `OH=OA+AH=3cm`
`ΔOHI` vuông tại `H` có `hat(O)=30^0`
nên `OI=2IH`
Theo Pytago , ta có :
`OI^2=OH^2+IH^2` hay
`(2IH)^2=OH^2+HI^2`
Suy ra `3IH^2=OH^2` do đó `3IH^2=9` suy ra `IH^2=3`
`ΔIAH` vuông tại `H` nên :
\(IA^2=IH^2+AH^2=3+1=4\left(cm\right)\\ \Rightarrow IA=2cm\)
Vậy bán kính đường tròn `(I)=2cm`