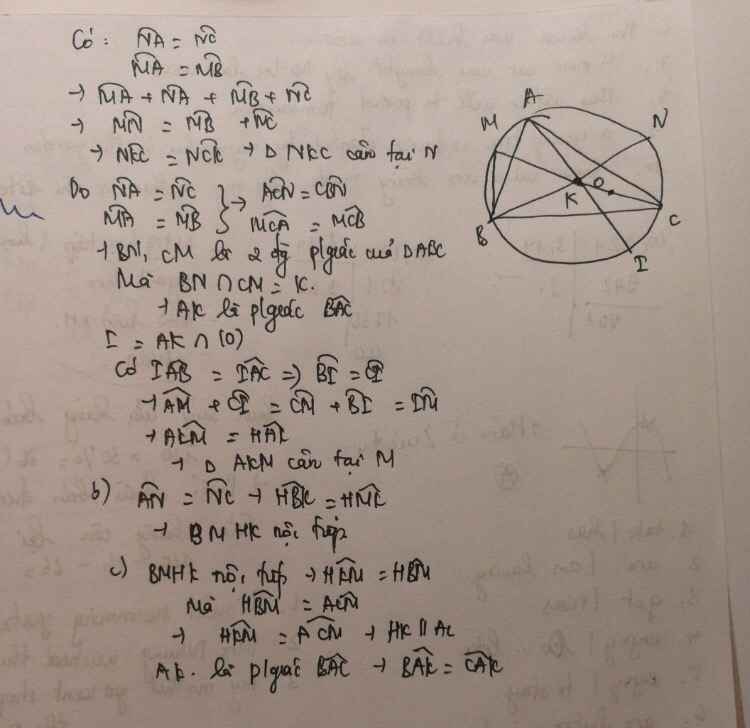Ôn tập góc với đường tròn
Các câu hỏi tương tự
Cho đường tròn (O) và 2 dây AB,AC sao cho AB<AC và O nằm trong góc BAC. Gọi M, N lần lượt là điểm chính giữa \(\stackrel\frown{AB}\) và \(\stackrel\frown{AC}\) .
MN cắt dây AB ở H, BN cắt CM tại K
a) C/m : tam giác NCK cân và Tam giác AMK cân
b) C/m : tứ giác BMHK nội tiếp
c) C/m : HK // AC và so sánh góc BAK và góc CAK
Cho đường tròn (O), đường kính AB cố định. Điểm I nằm giữa A và O sao cho AI = AO. Kẻ dây MN vuông góc với AB tại I. Gọi C là một điểm tùy ý thuộc cung lớn MN sao cho C không trùng với M, N và B. Nối AC cắt MN tại E.
a, C/m: Tứ giác IECB nội tiếp được trong một đường tròn. Xác định tâm đường tròn này.
b, C/m: ΔAME ∼ ΔACM
Cho tam giác ABC nội tiếp đường tròn (O) . Hai đường cao BD,CE cắt nhau tại H Và cắt đường tròn lần lượt ở M và N.
Cm: a, Tam giác AMN cân.
b, H và M đối xứng M qua AC và H đối xứng N qua AB.
c, OA vuông góc với DE
![]()
Cho tam giác ABC nhọn (AB bé hơn AC) nội tiếp (0). Vẽ bán kính OD vuông góc với dây BC tại I. Tiếp tuyến (O) tại C và cắt D tại M A)cmr : tứ giác ODMC nội tiếp B)cm: góc BAD bằng DCM C) tia CM cắt tia AD tại K , tia AB cắt tia CD tại E . Cm EK// DM
CẦN GẤP CÂU C NHÉ!!!
cho ΔABC có 3 góc nhọn (AB < AC) nội tiếp (O) .Hai đường cao BE,CF cắt nhau tại H
a, cm : tg AEHF nội tiếp được và Δ AEF đồng dạng Δ ABC
b, Đường phân giác góc FHB cắt AB,AB tại M,N
cm : \(\dfrac{MF}{MB}=\dfrac{NE}{NC}\)
c, Gọi I là trung điểm của MN
cm: Δ IEF cân tại I
GIÚP MÌNH NHA MIK ĐANG GẤP
Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O). Các đường cao BE, CF cắt nhau tại H. Gọi G là giao điểm của EF, BC. Đường thẳng đi qua A và vuông góc với GH tại I cắt BC tại M. Các tiếp tuyến với (O) tại B,C cắt nhau tại S.
a) Chứng minh tứ giác GFIC nội tiếp.
b) Chứng minh M là trung điểm của BC và tam giác AEM đồng dạng với tam giác ABS.
: Cho tam giác ABC nhọn (AB AC) nội tiếp (O), đường cao AD. Biết AD cắt (O) tại điểm thứ hai M, vé ME vuông góc với AC ( E thuộc AC), đường thẳng ED cắt Ab tại I.1) C/m tứ giác MDEC nôi tiếp.2) C/m MI vuông góc với AB3) c/m AB. AI AE. AC4) Gọi N là điểm đối xứng của M qua AB, F là điểm đối xứng của M qua AC, NF cắt AD tại H.a) C/m AM là phân giác của b) H là trực tâm của tam giác ABC.
Đọc tiếp
: Cho tam giác ABC nhọn (AB < AC) nội tiếp (O), đường cao AD. Biết AD cắt (O) tại điểm thứ hai M, vé ME vuông góc với AC ( E thuộc AC), đường thẳng ED cắt Ab tại I.
1) C/m tứ giác MDEC nôi tiếp.
2) C/m MI vuông góc với AB
3) c/m AB. AI = AE. AC
4) Gọi N là điểm đối xứng của M qua AB, F là điểm đối xứng của M qua AC, NF cắt AD tại H.
a) C/m AM là phân giác của ![]()
b) H là trực tâm của tam giác ABC.
Cho đường tròn tâm O .Kẻ đường kính AB và CD vuông góc với nhau . Gọi E là điểm chính giữa cung nhỏ CD .EA cắt CD tại F ;ED cắt AB tại M
a/ Các tam giác CEF và EMB là những tam giác gì ?
b/ chứng minh bốn điểm D , C, M ,B thuộc đường tròn tâm E .
cho tam giác ABC có ba góc nhọn (AB∠AC) nội tiếp đường tròn (o) vẽ tiếp tuyến tại A của đường tròn(o) cắt đường thẳng BC tại S tia phân giác của góc BAC cắt BC tại K và cắt đường tròn (o) tại E ,OE cắt dây BC tại I
a/ chứng minh:SA2 SB*SC
b/chứng minh:OE⊥BC tại I
d/vẽ tiếp tuyến SD của đường tròn (o) D là tiếp điểm D khác A . chứng minh:tứ giác SAOD nội tiếp được đường tròn và I
Đọc tiếp
cho tam giác ABC có ba góc nhọn (AB∠AC) nội tiếp đường tròn (o) vẽ tiếp tuyến tại A của đường tròn(o) cắt đường thẳng BC tại S tia phân giác của góc BAC cắt BC tại K và cắt đường tròn (o) tại E ,OE cắt dây BC tại I a/ chứng minh:SA2 =SB*SC b/chứng minh:OE⊥BC tại I d/vẽ tiếp tuyến SD của đường tròn (o) D là tiếp điểm D khác A . chứng minh:tứ giác SAOD nội tiếp được đường tròn và I