a) Vì = 90o (góc nội tiếp chắn nửa đường tròn) suy ra trong tam giác vuông MIB có tg
=
=
=>
= 26o34’
Vậy không đổi.
b) Phần thuận:
Khi điểm M chuyển động trên đường tròn đường kính AB thì điểm I cũng chuyển động, nhưng luôn nhìn đoạn thẳng AB cố định dưới góc 26o34’, vậy điểm I thuộc hai cung chứa góc 26o34’ dựng trên đoạn thẳng AB (hai cung ![]() và
và ![]() )
)
Phần đảo:
Lấy điểm I' bất kì thuộc ![]() hoặc
hoặc ![]() , I'A cắt đường tròn đường kính AB tại M'.
, I'A cắt đường tròn đường kính AB tại M'.
Tam giác vuông BMT, có tg =
= tg26o34’
Kết luận: Quỹ tích điểm I là hai cung ![]() và
và ![]()
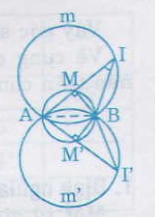
a) Vì \(\widehat{BMA}\)= 90o (góc nội tiếp chắn nửa đường tròn) suy ra trong tam giác vuông MIB có tg\(\widehat{AIB}\) = \(\dfrac{MB}{MI}\) = \(\dfrac{1}{2}\) =>\(\widehat{AIB}\) = 26o34’
Vậy \(\widehat{AIB}\) không đổi.
b) Phần thuận:
Khi điểm M chuyển động trên đường tròn đường kính AB thì điểm I cũng chuyển động, nhưng luôn nhìn đoạn thẳng AB cố định dưới góc 26o34’, vậy điểm I thuộc hai cung chứa góc 26o34’ dựng trên đoạn thẳng AB (hai cung ![]() và
và ![]() )
)
Phần đảo:
Lấy điểm I' bất kì thuộc ![]() hoặc
hoặc ![]() , I'A cắt đường tròn đường kính AB tại M'.
, I'A cắt đường tròn đường kính AB tại M'.
Tam giác vuông BMT, có tg\(\widehat{I'}\) = \(\dfrac{M'B}{M'I'}\) = tg26o34’
Kết luận: Quỹ tích điểm I là hai cung ![]() và
và ![]()









 . Kéo dài AC thêm một đoạn, CM=CB. Tìm quỹ tích điểm M.
. Kéo dài AC thêm một đoạn, CM=CB. Tìm quỹ tích điểm M.