CA/CB=2
nên CA=2CB
=>AC=2/3AB
DA/DB=2 nên DA=2DB
=>DA=2DB
CD=4cm nên CB+BD=4cm
=>1/3AB+AB=4
=>AB=3cm
CA/CB=2
nên CA=2CB
=>AC=2/3AB
DA/DB=2 nên DA=2DB
=>DA=2DB
CD=4cm nên CB+BD=4cm
=>1/3AB+AB=4
=>AB=3cm
Bài 1:Gọi M là điểm nằm trên đoạn thẳng AB sao cho MA/MB=1/2.Tính câc tỉ số AM/AB và MB/AB?
Bài 2:Cho đoạn thẳng AB.Điểm C thuộc đoạn thẳng AB; điểm D thuộc tia đối của tia BA sao cho CA/CB=DA/DB=2.Biết CD=4cm,tính AB?
Bài 3:Cho ∆ABC:Điểm D thuộc cạnh BC sao cho tỉ số BD/BC.Điểm E thuộc đoạn AD sao cho AE=2ED.Tính tỉ số AE/EC?
Cho tam giác ABC. Lấy điểm D thuộc đoạn AB, điểm E thuộc tia đối của tia CA sao cho BD = CE. Gọi giao điểm của DE và BC là M. CM: \(\dfrac{DM}{ME}=\dfrac{AC}{AB}\)
Cho đoạn thẳng AB= 6cm và điểm O thuộc đoạn thẳng AB sao cho OA= 4cm. Đường thẳng xy qua O. Lấy C thuộc tia Ox, OC= 3cm. Lấy D thuộc tia Oy, sao cho AD//BC. Tính OD và CD
Cho ΔABC. Từ D trên cạnh AB, kẻ đường thẳng song song với BC cắt AC tại E. Trên tia đối của tia CA, lấy điểm F sao cho CF=DB. Gọi M là giao điểm của DF và BC. Chứng minh \(\dfrac{DM}{MF}\)=\(\dfrac{AC}{AB}\)
Cho ΔABC có AB= 7,5cm. Trên tia AB lấy điểm D với \(\dfrac{DB}{DA}\)=\(\dfrac{1}{2}\)
a, tính DA,DB
b, Gọi DH,BK lần lượt là khoảng cách từ D,B đén cạnh AC. Tính \(\dfrac{DH}{BK}\)
c, Cho biết AK=4,5cm. Tính HK
Cho hình thang ABCD có AB //CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
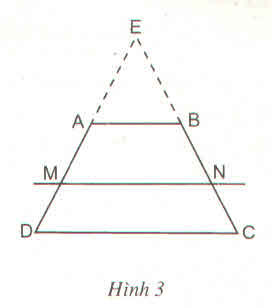
Chứng minh rằng :
a) \(\dfrac{MA}{AD}=\dfrac{NB}{BC}\)
b) \(\dfrac{MA}{MD}=\dfrac{NB}{NC}\)
c) \(\dfrac{MD}{DA}=\dfrac{NC}{CB}\)
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Cho tam giác ABC ,I là điểm thuộc D thuộc tam giác đó AI,BI,CI cắt BC,CA,AD tại M,N,P.CMR:
\\(\dfrac{MB}{MC}.\dfrac{NC}{NA}\dfrac{DA}{DB}\)
1. cho tam giác ABC có độ dài 3 cạnh là AB=8cm, AC=6cm,BC=12cm. trên tia đối của tia CA lấy điểm MM sao cho CM=3cm. Trên tí đối của tia CBlấy điểm N sao cho CN=6cm
a) C/M MN//BC
b) tính độ dài đoạn thẳng MN
2. Cho hình thang ABCD(AB//CD), GỌI I giao điểm 2 đường chéo AC VÀ BD. Qua I vẽ đường thẳng // 2 đáy hình thang cắt AD,BC lần lược tại Mvà N. C/M IM=IN
Cho tam giác ABC. Từ D trên cạnh AB, kẻ đường thẳng song song với BC cắt AC tại E. Trên tia đối của tia CA, lấy điểm F sao cho CF=DB. Gọi M là giao điểm của DF và BC. Chứng minh DM/MF=AC/AB