Bài 5: Trường hợp đồng dạng thứ nhất
Các câu hỏi tương tự
cho ∆ABC và ∆A'B'C' . Trên cạnh AB và AC lần lượt lấy điểm M và N sao cho: AM=A'B'=2cm , AN=A'C'=3cm A,c/m: MN//BC B,em có nhận xét gì về mối quan hệ giữa 3 ∆ là ∆ABC,∆AMN,∆A'B'C' mong mọi ng giúp:(((
Cho hai tam giác ABC và A'B'C' có kích thước như trong hình 35
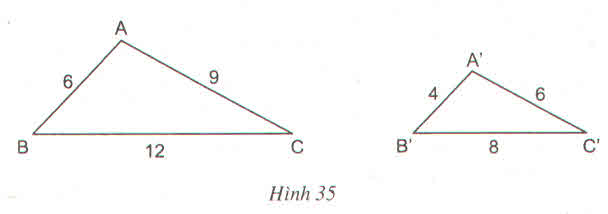
a) \(\Delta ABC\) và \(\Delta A'B'C'\) có đồng dạng với nhau không ? Vì sao ?
b) Tính tỉ số chu vi của hai tam giác đó ?
Cho ΔABC vuông tại A và ΔDEF vuông tại D có BC =10cm, AC = 8cm, EF= 5cm, DF=4cm
a) Tính AB,DE
b)Chứng minh \(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BD}{EF}\)
c) Chứng minh: ΔDEF đồng dạng với ΔABC
DeltaABC có D in BC sao cho dfrac{DB}{DC}dfrac{1}{2}. Kẻ DE // AC (E in AB). Gọi M là trung điểm AD. Gọi f là giao điểm EM và AC.
a, DeltaBED đông dạng vs tam giác nào trong hình? Tìm tỉ số đồng dạng.
b, DeltaADE đồng dạng vs tam giác nào trong hình? Tìm tỉ số đồng dạng.
Đọc tiếp
\(\Delta\)ABC có D \(\in\) BC sao cho \(\dfrac{DB}{DC}=\dfrac{1}{2}\). Kẻ DE // AC (E \(\in\) AB). Gọi M là trung điểm AD. Gọi f là giao điểm EM và AC.
a, \(\Delta\)BED đông dạng vs tam giác nào trong hình? Tìm tỉ số đồng dạng.
b, \(\Delta\)ADE đồng dạng vs tam giác nào trong hình? Tìm tỉ số đồng dạng.
Cho tam giác ABC vuông tại A có AB = 10cm; AC = 20cm. Trên cạnh AC lấy điểm M sao cho AM = 5cm
a)Tính độ dài BC, BM
b)Chứng minh \(\Delta\)ABC\(\sim\Delta\)AMB
3. Cho ΔABC (AB 3cm; AC 4,5; BC 6cm) và ΔDEF (DE 12cm; EF 9cm; DF 6cm)
a) Hai tam giác có đồng dạng không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác đó. So sánh tỉ số này với tỉ số đồng dạng của hai tam giác
4. Cho ΔABC ∼ ΔABC, biết chu vi ΔABC là 9cm và tỉ số đồng dạng là frac{1}{2} .Tính độ dài các cạnh của ΔABC biết: AB:AC:BC 2:3:4
Đọc tiếp
3. Cho ΔABC (AB = 3cm; AC = 4,5; BC = 6cm) và ΔDEF (DE = 12cm; EF = 9cm; DF = 6cm)
a) Hai tam giác có đồng dạng không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác đó. So sánh tỉ số này với tỉ số đồng dạng của hai tam giác
4. Cho ΔABC ∼ ΔA'B'C', biết chu vi ΔABC là 9cm và tỉ số đồng dạng là \(\frac{1}{2}\) .Tính độ dài các cạnh của ΔA'B'C' biết: AB:AC:BC = 2:3:4
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Trên cạnh OA lấy
điểm D sao cho 2
OD= 3OA
. Qua D vẽ các đường thẳng song song với AB, AC lần
lượt cắt OB, OC tại E và F
a) Chứng minh ΔDEF ∼ΔABC
b)Tính độ dài DE, AB biết hiệu độ dài hai cạnh đó là 12cm
c) Tính chu vi của Δ DEF, biết rằng tổng chu vi của Δ ABC và ΔDEF là 120cm.
Tam giác vuông ABC (\(\widehat{A}=90^0\)) có AB = 6cm, AC = 8cm và tam giác vuông A'B'C' (\(\widehat{A'}=90^0\)) có A'B' = 9cm, B'C' = 15 cm
Hỏi rằng hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không ? Vì sao ?
Cho M là điểm tùy ý nằm trong Δ ABC. Gọi D, E, F lần lượt là trọng tâm của các Δ MBC, MCA, MAB.
Chứng minh rằng: ΔDEF ∼ ΔABC.









