b: Xét ΔABC vuông tại B có \(\sin C=\dfrac{AB}{AC}=\dfrac{1}{2}\)
nên \(\widehat{C}=30^0\)
\(\Leftrightarrow\widehat{BAC}=60^0\)
a: Xét ΔEAC có \(\widehat{EAC}=\widehat{ECA}\)
nên ΔEAC cân tại E
hay EA=EC
1, Cho \(\Delta\)ABC(AB=BC). AD là tia phân giác của \(\widehat{A}\):
a, Chứng minh \(\Delta ABD=\Delta ACD\)
b, Chứng minh BD=CD
2, Cho \(\Delta ABC\)\(\perp\)tại A trên cạnh BC là điểm E sao cho BE=AB. Kẻ tia phân giác BD của \(\widehat{B}\)
a, Chứng minh \(\Delta ABD=\Delta EBD\)
b, Tính \(\widehat{DEB}\)
c, Gọi I là giao điểm BD và AE. Chứng minh BD\(\perp\)AE
Chú ý: Vẽ hình 2 bài
Cho tam giác ABC có \(\widehat{A}=110^0\), M là trung điểm của BC. Trên tia đối của tia MA lấy điểm K sao cho MK = MA
a) Tính số đo của góc ACK
b) Vẽ về phía ngoài của tam giác ABC các đoạn thẳng AD, AE sao cho AD vuông góc với AB và AD = AB, AE vuông góc với AC và AE = AC. Chứng minh rằng \(\Delta CAK=\Delta AED\)
c) Chứng minh rằng MA vuông góc với DE
Cho tam giác ABC có \(\widehat{B}=2\widehat{C}\). Tia phân giác của góc B cắt AC ở D. Trên tia đối của tia BC lẩy điểm E sao cho BE = AC. Trên tia đối của tia CB lấy điểm K sao cho CK = AB. Chứng minh rằng AE = AK ?
Cho \(\Delta\)ABC có \(\widehat{A}\) = \(90^o\), trên cạnh BC lấy điểm E sao cho BA=BE. Tia phân giác của \(\widehat{B}\) cắt AC ở D.
a, Chứng minh \(\Delta\)ABD=\(\Delta\)EBD
b, Chứng minh DA=DE
c, Tính số đo \(\widehat{BED}\)
d, Xác định độ lớn \(\widehat{B}\) để \(\widehat{EDB}\)=\(\widehat{EDC}\)
Bài 1. Cho \(\Delta ABC\) có \(\widehat{A}\)= 90o, trên cạnh BC lấy điểm E sao cho BE=BA. Tia phân giác của \(\widehat{B}\) cắt AC ở D
a) So sánh độ dài DA và DE
b) Tính số đo \(\widehat{BED}\)
Bài 2. Cho có OA=OB, tia phân giác của \(\widehat{O}\) cắt AB ở D. Chứng minh rằng:
a) DA=DB
b) OD \(\perp\) AB
Bài 2: (Vẽ hình) Cho \(\widehat{xOy}\). Trên tia \(Ox\) lấy điểm \(A\), trên tia \(Oy\) lấy điểm \(B\) sao cho \(OA=OB\). Gọi \(C\) là 1 điểm trên tia phân giác \(Oz\) của \(\widehat{xOy}\). Chứng minh rằng:
a, \(AC=BC\)
\(\widehat{xAC}=\widehat{yBC}\)
b, \(OC=OB\)
Cho \(\Delta\)ABC. Gọi M là trung điểm của BC. Trên tia AM lấy điểm D sao cho M là trung điểm của AD. Nối B với D, C với D.
a, Chứng minh AC = BD, AC //BD;
b, Cho \(\widehat{BAC}\) = \(90^0\). Tính \(\widehat{BDC}\)
cho \(\widehat{xOy}\) lấy A,C \(\in\) Ox sao cho OC<OA. Trên tia Oy lấy B và D sao cho OB=OA,OD=AC a, c/m:AD=BC và \(\Delta ABC=\Delta BAD\) b,Gọi I là giao điểm của AD và BC cho biết IA=IB . Chứng minh OI là tia pg góc xOy
Xét bài toán :
"Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng AB //CE"
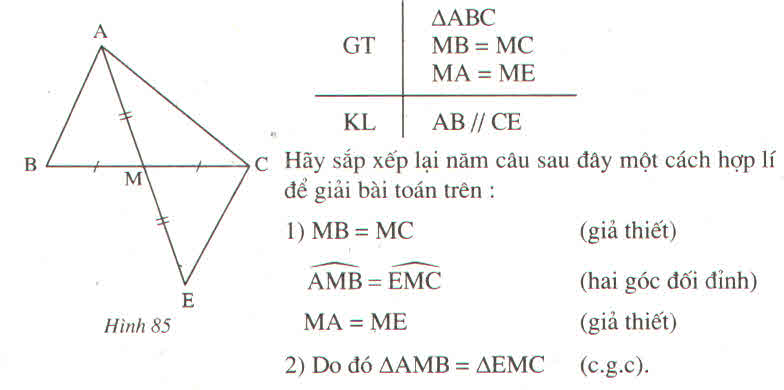
3) \(\widehat{MAB}=\widehat{MEC}\Rightarrow\) AB // CE (có hai góc bằng nhau ở vị trí so le trong)
4) \(\Delta AMB=\Delta EMC\Rightarrow\widehat{MAB}=\widehat{MEC}\) (hai góc tương ứng)
5) \(\Delta AMB\) và \(\Delta EMC\) có :
Lưu ý : Để cho gọn, các quan hệ nằm giữa, thẳng hàng (như M nằm giữa B và C, E thuộc tia đối của tia MA) đã được thể hiện ở hình vẽ nên có thể không ghi ở phần giả thiết
