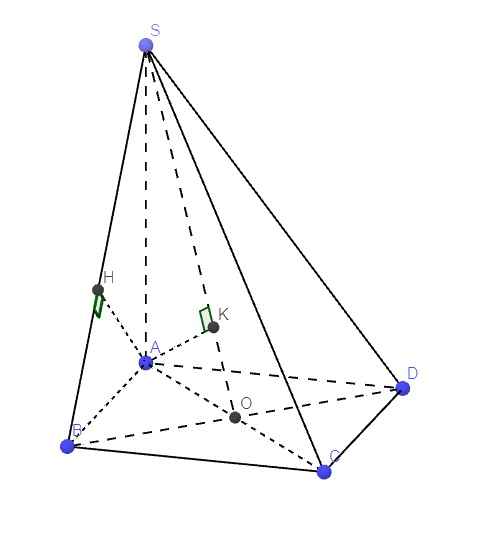
a.
Từ A kẻ \(AH\perp SB\) (1)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) (2)
(1);(2) \(\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
Áp dụng hệ thức lượng trong tam giác vuông SAB:
\(AH=\dfrac{SA.AB}{SB}=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{2a\sqrt{5}}{5}\)
Do \(AD||BC\Rightarrow AD||\left(SBC\right)\Rightarrow d\left(A;\left(SBC\right)\right)=d\left(D;\left(SBC\right)\right)\)
\(\Rightarrow d\left(D;\left(SBC\right)\right)=\dfrac{2a\sqrt{5}}{5}\)
b.
Gọi O là giao điểm 2 đường chéo \(\Rightarrow OA\perp OB\) (t/c hình vuông)
Từ A kẻ \(AK\perp SO\) (1)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BO\Rightarrow BO\perp\left(SAO\right)\)
\(\Rightarrow BO\perp AK\) (2)
(1);(2) \(\Rightarrow AK\perp\left(SBD\right)\) \(\Rightarrow AK=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng trong tam giác vuông SAO:
\(AK=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{2a}{3}\)
Do \(\left\{{}\begin{matrix}AC\cap\left(SBD\right)=O\\AO=CO\end{matrix}\right.\) \(\Rightarrow d\left(C;\left(SBD\right)\right)=d\left(A;\left(SBD\right)\right)=\dfrac{2a}{3}\)