Question

Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm của đường trung Xác định tâm và bán kính của đường tròn ngoại tiếp mỗi tam giác sau:

a) Tam giác đều MNP có cạnh bằng 4;

b) Tam giác EFG có EF = 5 cm; EG = 3 cm; FG = 4cm.

 

Answer 1

a) Vẽ đường cao MH của  giác  MNP, gọi O là điểm nằm trên MH sao cho

OM = \(\frac{2}{3}\) MH.

Do tam giác MNP đều nên O vừa là trọng tâm vừa là giao điểm của ba đường trung trực.

Bán kính đường tròn ngoại tiếp tam giác MNP là:

R = OH = \(\frac{{a\sqrt 3 }}{3} = \frac{{4\sqrt 3 }}{3}\) (cm).

b)

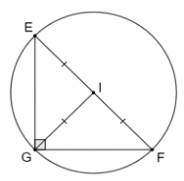
Ta có: \({5^2} = {3^2} + {4^2}\) nên \(E{F^2} = E{G^2} + F{G^2}\)

Suy ra tam giác EFG vuông tại G.

Gọi I là trung điểm của cạnh huyền EF. Ta có GI là đường trung tuyến ứng với cạnh huyền của tam giác EFG vuông tại G,

suy ra IG = IE = IF = \(\frac{{EF}}{2}\) = 2,5 cm

Vậy đường tròn tâm I bán kính 5 cm ngoại tiếp tam giác EFG.