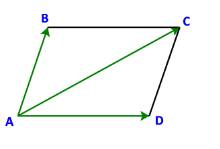
Ta có: \(\overrightarrow {AM} = - \overrightarrow {MA} ,\;\overrightarrow {DM} = - \overrightarrow {MD} \)
\( \Rightarrow \overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MB} + \overrightarrow {AM} = \overrightarrow {AM} + \overrightarrow {MB} = \overrightarrow {AB} \)
Tương tự ta có: \(\overrightarrow {MC} - \overrightarrow {MD} = \overrightarrow {MC} + \overrightarrow {DM} = \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {DC} \)
Mà \(\overrightarrow {AB} = \overrightarrow {DC} \)(do ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD} \) (đpcm)