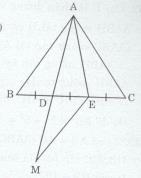
+ Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại \(A.\)
=> \(\widehat{ABC}=\widehat{ACB}\) (tính chất tam giác cân).
Hay \(\left\{{}\begin{matrix}\widehat{ABD}=\widehat{ACE}\\\widehat{ABE}=\widehat{ACD}\end{matrix}\right.\)
Xét 2 \(\Delta\) \(ABD\) và \(ACE\) có:
\(AB=AC\left(gt\right)\)
\(\widehat{ABD}=\widehat{ACE}\left(cmt\right)\)
\(BD=CE\left(gt\right)\)
=> \(\Delta ABD=\Delta ACE\left(c-g-c\right)\)
=> \(\widehat{BAD}=\widehat{EAC}\) (2 góc tương ứng) (1).
+ Vì \(\widehat{AEB}\) là góc ngoài tại đỉnh E của \(\Delta ACD.\)
=> \(\widehat{AEB}>\widehat{ACD}\) (tính chất góc ngoài của tam giác).
Mà \(\widehat{ABE}=\widehat{ACD}\left(cmt\right)\)
=> \(\widehat{AEB}>\widehat{ABE}.\)
=> \(AB>AE\) (quan hệ giữa góc và cạnh đối diện trong tam giác).
Trên tia đối của tia DA lấy điểm M sao cho DM = DA.
Xét 2 \(\Delta\) \(DME\) và \(DAB\) có:
\(DM=DA\) (do cách vẽ)
\(\widehat{MDE}=\widehat{ADB}\) (vì 2 góc đối đỉnh)
\(DE=DB\left(gt\right)\)
=> \(\Delta DME=\Delta DAB\left(c-g-c\right)\)
=> \(\widehat{DME}=\widehat{BAD}\) (2 góc tương ứng) (2).
=> \(ME=AB\) (2 cạnh tương ứng).
Mà \(AB>AE\left(cmt\right)\)
=> \(ME>AE.\)
Xét \(\Delta AEM\) có:
\(ME>AE\left(cmt\right)\)
=> \(\widehat{DAE}>\widehat{DME}\) (quan hệ giữa góc và cạnh đối diện trong tam giác) (3).
Từ (1), (2) và (3) => \(\widehat{DAE}>\widehat{BAD}=\widehat{EAC}\left(đpcm\right).\)
Vậy trong ba góc BAD, DAE, EAC thì góc DAE là góc lớn nhất.
Chúc bạn học tốt!










